在上一节,我们展示了一群人如何选择一个公平的随机数。在这一节里,我们将讨论如何用比特币来产生一个对任何人都公平的公共随机数。为什么我们需要一个公共随机数?让我们先看一下几个现实中已经存在的依赖公共随机数的案例。
NBA新人选秀
其中一个例子就是每年春天的美国NBA联赛的新人选秀大乐透。NBA联盟中所有的30支球队聚集在一起,根据上赛季每个球队的赛季排名增加相应的权重,随机选择球队选秀顺序。在1985年,联盟首次采取这种方法进行选秀,乐透选秀的过程通过电视现场直播,包含球队名字的信封在一个透明的转盘里被充分打乱,委员会专员随后去挑选这些信封。因为纽约尼克斯(Knicks)队获得了当年的状元秀中锋帕特里克·尤因(Patrick Ewing),最终尤因也确实成为NBA名人堂的一员,当时这个乐透的产生引起了不小的争议。由于那次的乐透发生在纽约,其他球队的球迷宣称整个过程被人操纵,并偏向尼克斯队。
有很多有关NBA是如何操纵选秀过程的阴谋论,比如著名的“折角”论(“bent corner” theory)是说包含有尼克斯的信封有一个角被故意折弯了,这样委员会专员通过触摸就可以分辨出哪个信封是尼克斯的。另外一个论调是说尼克斯的信封之前被放在了冷冻室里,这样专员可以通过选择一个手感比较冷的信封来挑选出尼克斯队。这些论调都反映了一个事实,这种类型的选择要做到绝对公平是非常困难的,有很多合乎推理的作弊空间,想象一下一个职业魔术师的巧手可以做些什么!直到今天,选秀乐透每年都会举行,但每一次都充斥着各种阴谋论和谣言,以说明选秀并不是绝对公平的。
美国军队选秀
另一个更加严肃的案例是1969年的美国征兵选秀,用于决定哪些年轻人会去参军,大部分被选中的人事后都被派去参加了越南战争。同样使用了一个类似于NBA选秀的方法,由美国国会派出的代表来主持选秀并通过电视直播(如图9.6)。他们在一个大的塑料桶中放了很多小球,每个小球包含了一个数字,然后轮流从桶中把这些数字小球取出来,根据数字所代表的生日来决定优先级,根据这个优先级挑选合格的年轻人参军。

图9.6 1969年(越战)军队选秀
1969年的这次征兵选秀,是首次在全国范围内采用乐透方式进行选秀。其目的是通过避开数以千计的本地征兵委员会,以使选拔过程更加公平,并且向公众公开这个过程。但遗憾的是,这个选秀乐透也演砸了,不到一个星期,概率专家通过数据调查分析注意到了一个特别的模式(如图9.7所示):出生于下半年的人被选中的优先级较低。虽然这种差异非常细微,但是从概率统计上是非常显著的,说明这不太可能是偶然事件。当他们回看现场录像的时候,发现每次转动转盘的次数恰恰都是偶数次,这意味着一开始是上层的小球有较大的概率一直留在上层,说明为了形成随机抽签的混合程序并不充分。
这两个案例都证明了,设计一个公众认可的随机过程并由此产生一个认可的公共随机数,是十分困难的。无论你采用什么方法,总有人怀疑你作弊。风险在于:这个随机过程可能会被操作——即便这个过程是真正随机的,但公众并不信任它。[1]

图9.7 1969年征兵选秀的概率统计偏差
注:x轴代表日期,y轴代表选秀号码。
密码学“信号塔”
由于成本低,并且大众易于理解,用转盘、抛硬币、掷骰子等方法去展示公开随机性,在历史上一直比较普遍。但是这些方法非常难以审计,因此并不适用于大范围的场景。即使整个过程从视频上看起来是合法的,人们也有理由去怀疑乐透的执行者可以使用“魔术师之手”去操纵结果。
那么,通过密码学的办法,我们是否可以做得更好?这里,我们用密码学“信号塔”(cryptographic beacons)来特指一个提供公共随机源的服务。我们的想法是“信号塔”会源源不断地在一个固定的频率产生随机数,并且没有人可以预测这些随机数。只要大家同意这一点——没人可以预测这个信号塔的下一个输出,那么大家就都可以相信其生成的是一个真正的随机数。
一个完美的密码学信号塔可以服务于各种公开乐透项目,比如上面两个例子。如果你想要在本地的俱乐部玩一个宾果(Bingo)游戏[2],你再也不需要用一个大的转盘来产生随机性了。只要每个人都信任信号塔,就不要用物理的方法来展示随机性了,这会省去很多麻烦。
密码学专家提出了很多其他的公共随机源的应用方案,包括投票系统、零知识验证、分割选择协议等。如果你有一个完美的密码学信号塔,其中很多方案都会变得非常简单有效。但遗憾的是,截至目前,我们还没有找到一个完美的方案去打造这样一个信号塔。
NIST信号塔
NIST,即美国国家标准与技术研究所(National Institute of Standard and Technology)。从2011年开始,NIST运行了一个它们自己的信号塔服务。它们声称用了一个非常复杂的实验室装置来产生随机数,甚至动用了两个纠缠态光子。由于随机数是由量子力学现象产生的,那么理论上这个数字可以保证非常强的随机性。如果你认可海森堡不确定性原理(Heisenberg uncertainty principle)和其他一些被广泛接受的物理学原理,那么你就会相信这个信号塔产生的数是真正随机的,并且不可预测。NIST信号塔服务可以每60秒产生一个附带有数据签名的随机数,并提供一个非常便利的程序接口——服务可以通过网页来访问并返回随机数。
从某种意义上说,NIST信号塔代表了从物理上展示随机性的极限,但无法解决一个基本的信任问题——你必须信任NIST确实是通过它们所宣称的这些程序来产生随机数的,你必须信任在马里兰州的某一个建筑里面,NIST确实用它们的实验室来产生这些随机数,而不是伪造的,你还必须信任它们确实没有能力故意重写其中一些随机数。
打造一个信号塔的其他潜在方法:自然现象
我们是否可以使用一些每个人都可以观测到的自然现象来实现信号塔?或者我们可以使用天气的一些细节,比如在某天某个特定地点的温度,或者是风力的强度,或者是否会下雨。当然,我们有能力去提前预测天气,但是预测的结果并不是非常精确,所以我们可以使用这些测量值的“最低有效位”。但是这个方法也有局限性,那就是需要所有的参与者在同一个地点做同样的测量。
为了避免这个问题,我们可以利用太阳黑子,一种太阳表面的爆发活动(见图9.8)。另外一个例子是宇宙背景辐射,通过广播天线,你可以从地球上的任意一点都可以监测到这个数据,而且每个人都可以读取到同样的数值。这些都是超大范围发生的现象,很容易向公众证明没有其他人可以操纵这个过程。想象一下,某人穿越宇宙到达太阳表面,然后用某种办法去影响太阳黑子现象,而其目的仅仅是为了操纵地球上的某个乐透项目,这显然是不现实的。所以上述这些方法都有很好的特性:公众可观测性、可防止被操纵性,以及一个可接受的不可预测性。

图9.8 NASA太阳黑子照片
但上述这些方法都有一个共同的问题,就是生成随机数太慢了。例如,如果随机信号是当日最高温度,那么你每天只能获取一次这样的数值;太阳表面也不是经常变化,在很多密码学应用中,随机数通常作为伪随机数发生器(Pseudo-Random Generator,简称PRG)的输入,从安全角度考虑,这些输入通常需要达到80比特位长度,甚至更多,但如果以天气或者天文学为数据源,那我们可能需要很长时间才能积累到80位长度的随机数。
另外,观测太阳黑子现象这种方法还需要专业技能,所以你还需要依赖一些可信任的专业观测者来获取这些测量数据。由于有很多这样的可信任的观测者,我们也希望他们“互相之间有诚信”。信号塔的应用者,或者说是这些应用的用户,可以随时选择并替换观测者。这个特性被称为“信任的敏捷性”,相比于NIST是提供信号塔服务的单一机构,这个特性更加优越。
还有更深层次的问题,虽然这个问题看起来可能微不足道,那就是,我们是否可以找到一个方法,它可以使一个现实世界的观测数据——例如温度、太阳黑子图——转变为一个数据字符串,并且它还需要保证每一个观测者都获得相同的字符串?我们可以尝试数字化这个观测数据:比如,我们用华氏度来描述温度,并使用第一个十进制数位作为信号塔的输出,但是除非每一个观测者的温度计都是不可思议的精准,否则就会出现下面的情形,有些观测者读取的温度(比如)是62.7,而另外一些人读取的则是62.8。目前看来,不管我们选择哪种自然现象或者采用哪种协议,我们都会遇到这种“极端情况”。对于一个密码学信号塔,即使测量值出现非连续性的可能性非常小,那也是无法接受的,因为这有可能使得PRG产生的随机数变得完全不同。
金融数据
还有一个类似的想法是使用金融数据作为数据源,比如股票市场价格指数。同样,这些是公开的可观测的数值,而不像自然现象,这些金融数据本身就是用数字来呈现的,所以不会因为观测者不同,产生数据不一致的问题;同时,我们有很好的理由相信,股票价格的小波动是很难预测的:如果你可以预测纽约证交所某一只股票的交易价格,并且精确到美分级别,你就会成为一个非常赚钱的日内交易员。某些人可以通过买卖股票,去操纵股票价格到某一个特定的数值,但这需要巨大的成本。
但是,这种方法也需要依赖某一个信任方,比如股票交易所。即使股票交易所本身有很强的意愿去建立自己的诚信,但如果让它们操纵一个非常有利可图的乐透,那么它们就有可能去尝试改变股票价格(例如,通过插入自己的买卖单)。
截至目前讨论的方法,似乎很难去规避信任方的问题,而这个信任方却是可以在整个过程中的某些关键环节对结果施加重要影响的。
用比特币作为一个“信号塔”
幸运的是,把中央权威从数据交换协议中剥离出来,在之前认为几乎是不可能的任务,而比特币是很有希望实现这一任务的技术,而这也是本书的中心思想之一。我们是否可以把比特币作为一个生成随机数的“信号塔”呢?我们想要从比特币的区块链里摘取随机数,与此同时保留比特币所有去中心化的特点,正是这些特点使比特币如此吸引人。
我们回忆一下,矿工必须计算大量的随机哈希函数来找到一个有效区块。或许这意味着没有人可以不经过挖矿工作就能预测或是影响下一个区块的生成。当然,任何一个区块的哈希函数结果的最初几个字节都是零,但是在合适的假设下,唯一可以预测剩余位数的比特值的方法可能是找到一个胜出有效区块,然后选择性丢弃它(见图9.9)。
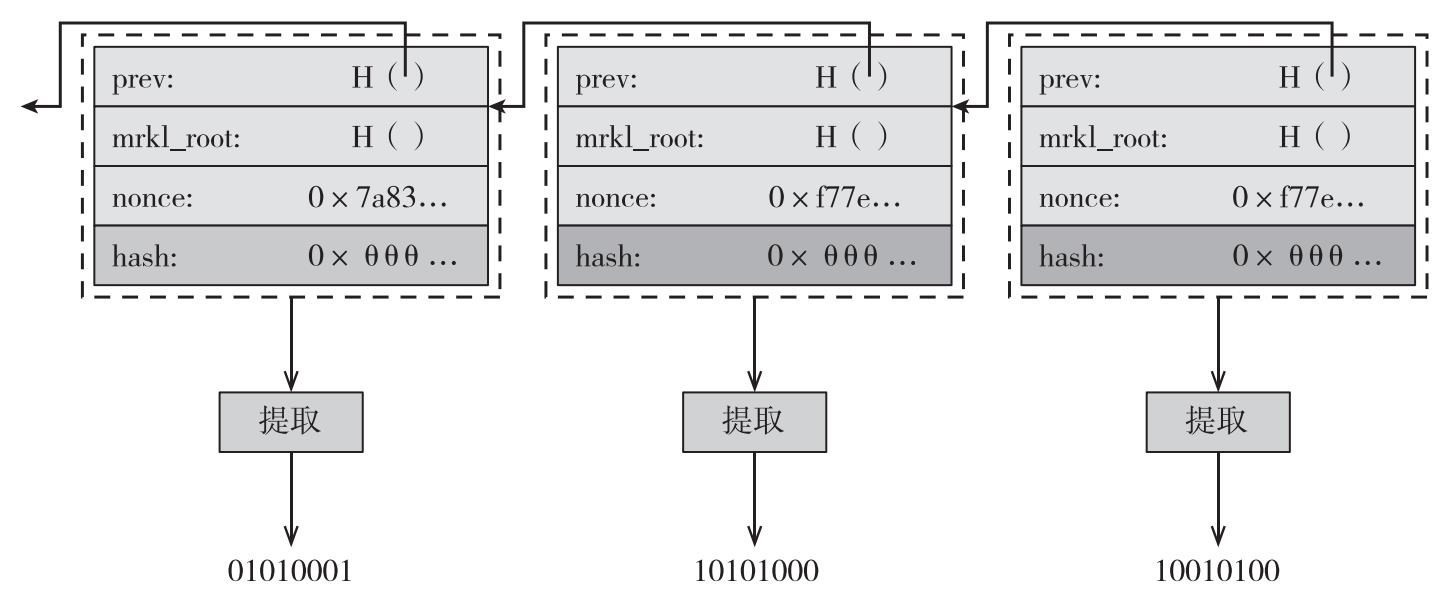
图9.9 比特币像灯塔一般
注:我们可以通过使用随机提取功能,提取公共随机数据,标注区块链上的各个区块。
这样一来,把区块链变成一个随机数“信号塔”成了一件简单的事。在区块链上的每一个区块上,我们在区块头部设置一个“随机数抽取器”。随机数抽取器,其实就是一个哈希函数,这个哈希函数把所有的输入随机熵均匀地压缩成一个随机字符串。每次只要发表一个区块,我们就有了一个新的随机信号输出。
评估比特币“信号塔”的安全性
假设你参加一个乐透抽奖,这个抽奖的结果是由未来将要产生的、一个预先设定的、位于高度h的某个区块的输出所决定的。这个乐透抽奖有N个参与者,每个参与者都下注了B个比特币,如果你也是一名矿工,我们再假设,你幸运地找到了一个区块h的函数解谜的答案,你就可以选择发表或是不发表这一区块。如果你不喜欢从这个区块里产生的抽奖的结果,你可以轻易地丢弃这一区块,然后让其他找到这个区块的人来决定这个抽奖结果,但同时,你必须放弃因为找到这个区块所带来的收入。
让我们计算一下,下注的数额B值需要多大,才值得考虑放弃区块本身的奖励。如果你成功地找到了一个位于高度h的区块来决定抽奖的结果,然后意识到,如果你发表了这个结果,你肯定会输掉抽奖;如果你扔掉这块,你还是有1/N的概率来赢得B×N比特币,这就意味着,如果你期望的抽奖奖励(1/N)×B×N比特币比挖矿所获得的25个比特币奖励要大的话,那么放弃区块奖励是合理的(在2015年,如果不考虑交易费的话,区块奖励大概是25个比特币),所以如果B大于25,这种丢弃策略就是有利可图的。在2015年中旬,25个比特币价值大约在5 000美元左右。所以如果每个玩家下注不到5 000美元的话,并且假设每个玩家都是理智的,那么这个乐透抽奖是可以抵抗放弃有效区块这种攻击的。
另一大优点是这是一个完全去中心化的信号源,没有一个中心化的信托方。比起其他几个信号源的方案,它的处理速度相当快,大概每10分钟就产生一个输出。然后通过上述的简单模型,我们可以估计一个攻击者想要操纵信号源输出所需要付出的代价。
用比特币作为信号塔办法的一个缺点是,不能精确定时。比如,假设我们想要在明天正午读取这个信号源的值,但我们无法知道哪个区块在哪个时点会生成最新的一个区块。虽然平均来说,在正午之前或之后的10分钟内一定会有一个区块被公布,但这还是会有误差。如果我们想降低目标区块在一个短分叉事件中丢失的可能性,我们还要对有可能发生的延迟有所准备。在比特币世界里,通常情况下要等6个区块(60分钟)后,才能确信这个信号值是真正地被确认了。
另一个缺陷是,相对来说,操纵这个信号值所需的代价可能还是太低。如果我们用这个方法来实行NBA选秀,由于其中可能涉及几千万美元利益,球队顿时就有了贿赂矿工来操纵选秀过程的动力。所以,当涉及巨额资金时,这个方法是否有效仍值得探讨。
最后,我们的安全评估忽略了一些现实生活中的因素。比如,对于加入某一个矿池的矿工来说,丢弃一个有效区块并不会让他损失很多钱,因为他们是根据贡献算力的比例,而不是区块来领取奖励的。所以,比特币信号塔目前还是一个有趣但没有被证明的想法。
脚本语言对信号塔的支持
如果我们扩展比特币的脚本语言功能,加入一个特殊的操作码(opcode)来读取比特币信号呢?按照最初的设计,现在的比特币脚本语言没有任何办法去实现任何随机性,因为矿工必须验证脚本,而且一个脚本的有效性需要获得所有矿工的认可,但如果我们用了信号塔产生的随机数,由于这是一个可被证明的公共随机数,把这个随机数加入交易脚本中,矿工就容易随机性地达成共识。
假设我们有一个操作码可以做一个随机的决定,这个决定是基于上个区块的信号塔输出的。我们可以把整个复杂的抽奖数据协议用一个脚本来替代——读信号塔的随机数值,然后把该输出分派到n个密钥中的一个。这需要有多回合的数据协议安全保证或是有时效的函数约定。
这个想法的一个缺点是,为矿工操纵抽奖提供了可能性,如果他们发觉挖到的这一个区块里的交易会让他们输掉这个抽奖,他们就会简单地将抽奖交易延迟至后面的一块出现。但是我们可以对信号塔的操作码做一个小小的调整来防御这类攻击,也就是说,你不是用上一个区块,而是使用某一个特定高度的区块所产生的信号塔随机数。
[1] 所以一个公平的不受操纵的公共随机源是一个公共福祉,而比特币可以做到这一点,因为它是去中心化的。——译者注
[2] Bingo是一种填写格子的游戏,在游戏中第一个成功者以喊“Bingo”表示取胜而得名。——译者注
