如果原子研究不能适合空间和时间,那它整个目的就失败了,我们也就不知道它的作用究竟是什么。
——薛定谔
《致维里·维恩》,1926年8月25日
对于时间箭头的存在,量子力学给了我们饶有兴趣的启示。如我们将会看到的,它认为时间的流逝是由某种非常简单的事情决定的:即我们自己对于变化的观测。它揭开了原子世界的奥秘,显示了有一种极其微小的粒子(长寿K介子),其存在表示时间是不可逆的。但是物理学家们仍然在为此争论不休:这确实是一个基本线索呢,还是一种风马牛不相及的东西。有一件事倒是很清楚——量子世界中到处都是问题和佯谬。例如,这个新理论在许多方面仍然在步它的前任的后尘,时间似乎是既可以向前又可以向后。它认为事件会无休止地重复出现,但同时也支持这样的观点,即锅里的水决不会自发地沸腾。它认为,一只猫在同一时刻既是活着又是死了,而且有些东西在同一瞬间,既是无处不在又是无处在。它是一种如此奇怪的理论,许多帮助它创立的科学家——其中包括爱因斯坦——后来极力要与它脱离关系。在它创立了几十年之后的今天,对于量子论究竟意味着什么,仍然有许多不同的看法。
量子论涉及的是物质在最微小的尺度上的性质,这其中包括原子,它是化学元素的最小单位。在试图描述世界在这种微观层次上的行为时,我们发现牛顿力学不能用了。和它在相对论涉及的高速大质量物体情况下的失效相比,牛顿力学在处理微观世界情况下的失效更为明显。与此相反,量子论却在原子层次取得了非凡的成功。我们对化学反应、激光、晶体管和作为现代计算机技术基础的二极管的详尽知识,都依赖于量子论。今天,原子的存在看来是没有争议的了——原子和分子的图像甚至可以借助于场离子、电子或者扫描隧道显微镜而看到(见彩图页)。但是人们很容易忘记,对原子存在的争议其实还是不久以前的事。虽然原子论的思想古代就产生了,但多少个世纪以来,它一直受到压制。
原子的史话也许始于大约公元前500年爱琴海的一个海港阿布德拉。两位原子论的先驱者,一位是哲学家卢西普斯(Leucippus),另一位是他的学生,阿布德拉的德谟克利特(Democritus of Abdera)。他们的观点与现代科学观点并没有太显著的差异。他们认为,世界是由微小的、看不见的而且不能够再缩小的物体所组成——这些物体只是在外形和大小上有区别——它们在无限的真空中处于永恒的运动状态。他们把这种物质实体称之为原子,意思是不可再分的,并且认为一切物体,从桌子到海龟,都是由于原子的偶然碰撞而形成的。原子论者还用原子来解释感觉现象,例如味觉和嗅觉。不幸的是,由于柏拉图和亚里士多德的影响,原子论被人们遗忘了。这几位西方哲学之父主张,物质可以被无限地分割,不存在不能再被进一步分割的最小单元。原子论于是被打垮,在阴影之下度过了2500年。
为什么原子论又东山再起了呢?这主要归功于一位名叫道尔顿(John Dalton)的教友派教师,他1766年出生于昆布兰郡的依格列斯菲尔德城。他在1808~1827年写的题目为“化学哲学的新体系”的两卷体专著,使原子论得以新生,并且成了现代化学的奠基著作。道尔顿认识到,原子有助于解释越来越多的科学现象,包括气体的行为和一种物质到另一种物质的化学变化。道尔顿认为,原子是物质最小的不可再分的单元,并仍然具有这种物质的化学性质。他主张,化学反应只不过是这些物质的基本“砖块”的分离和组合。今天我们通常把这些“砖块”称为分子——它们是原子可以参与化学反应的最低组合。例如,水分子就是由两个氢原子和一个氧原子组成的。
开始的时候,其他化学家对道尔顿的主张将信将疑。他们了解他的想法,但是并不认为原子确实存在,所以只是把原子作为一种方便的工具,用来解释他们的实验数据。法国化学家杜马斯(Jean Baptiste Dumas)甚至说,“假使我能做主的话,我会把原子这个词从科学上抹掉。”然而过了一段时间,化学家和物理学家们开始认识到,他们已经积累了许多独立的证据,这些证据毫不含糊地倾向于原子论。当时,争论的焦点主要是气体和所谓的动力论,即用原子和分子来解释气体性质的理论。物理学家们,像麦克斯韦和玻耳兹曼,提出了简单的模型来解释气体对容器的压力。他们把气体形容为像台球那样的一群刚性球的集合,它们不停地快速撞击容器的器壁,这种碰撞过程可以用牛顿力学来描述。气体的性质用构成气体的原子和分子的运动来解释。压力可以很容易地从刚性球碰撞容器壁的速率计算出来。热是分子快速随机运动的结果:气体越热,分子的运动也越快。
但是对于像马赫和德国物理化学家奥斯特瓦尔德(Wil-helm Ostwald)这样的死硬派原子论反对者来说,这些还仍然不足以说服他们。作为实证主义者,他们强调说,谈论一个无法直接看到的世界是毫无意义的。原子论者所需要的,是能够直接展现在怀疑者眼前的分子作用事例。到1905年他们认识到,有一个事例早就可以用了,它在道尔顿那个时代就已经被发现。这就是所谓的“布朗运动”——悬浮在水中的很小的花粉(以及尘埃或煤烟)颗粒,像跳舞那样的运动。早在1827年,苏格兰植物学家布朗(Robert Brown)就曾经在显微镜下观察过这种作用,但是对此一直没有令人信服的解释。直到爱因斯坦,才对这个问题的研究做出了独特而卓越的突破。他解释说,布朗运动是由于悬浮的颗粒,与它们周围看不见的水分子的随机碰撞。
这是物质原子论的一个有力证明。但是那时候经典的原子概念——像卢西普斯和德谟克利特所设想的那样——已经过时了。它已经在19世纪将近结束的时候,被放射性的发现所取代。1895年,德国物理学家伦琴(Wilhelm Rontgen)偶然间发现了一种神秘的射线,他把它叫做X射线。第二年,法国的贝克勒尔(Henri Becquerel)在研究X射线的时候,探测到有很强的辐射从铀的化合物中发射出来。由波兰化学家玛丽·居里以及其他人所做的后继工作,把这些零散的发现汇总到一起,从而发现有些元素的原子,可以衰变为化学性质完全不同的其他元素。放射性元素的这种变化——几乎类似于中世纪的炼金术士们所梦寐以求的——在1902年由卢瑟福(Ernest Rutherford)和索迪(Frederick Soddy)用定律的形式清楚地表述出来。从这一点上说,现代的物质原子论已经同古代沿袭下来的观念断绝了关系,因为现代原子论表明,原子本身具有结构,而且可以被进一步分割。
原子结构与经典物理学的失效
在20世纪的头10年间,接二连三的有关原子结构的发现,就像是一场竞赛。无疑这其中最重要的实验,是盖革(Ha ns G eige r)和马斯登(M arsden)在卢瑟福指导下,于1909年在曼彻斯特大学所做的那次实验。它的结果是非凡的,使人们第一次有了印象,一个原子看起来是什么样子;而且开辟了通向新的物质观的途径。这两个人用放射性物质产生的阿尔法粒子束(在放射性衰变过程中辐射出的带正电荷的粒子),去轰击金箔。大多数粒子直接穿过这很薄的箔片,只产生很小的偏转。然而有极少数粒子,却朝正好与粒子束相反的方向反弹回去。卢瑟福说,这是他从来没有遇到过的最难以置信的事情:“它差不多就是你用大口径的火炮去轰击一张薄纸,而炮弹却反弹回来把你打中。”他对这一散射结果的解释是,阿尔法粒子可能是被质量很大、但体积很小的原子核碰撞回来,原子核带正电荷并位于箔片上每一个金原子的中心。
卢瑟福的著名原子模型是在1910年圣诞节期间发表的。在他这个模型中,带负电的电子就像一个微型太阳系中的行星那样,围绕原子核作轨道运行。原子的大部分是空的,原子的大小决定于最外边的电子轨道。原子核的半径(等价于太阳的半径)大约是一千万亿分之一米,电子运动区域的半径大约是一百亿分之一米。人们很快就认识到,放射性是由于从原子核内部辐射出粒子,这跟着表明,原子核也同样具有某种内部结构。
鉴于牛顿物理学的种种成就,我们自然地相信,电子的运动也应遵从牛顿的决定性的方程。如果牛顿力学对板球成立,为什么会对板球中的原子和电子不成立?用这种思维方式可以得出许许多多的预言,其中大多数是可以用实验来验证的。
然而,在应用到原子吸收和发射光线的情形时,经典方法就失效了。按照麦克斯韦的电磁理论和牛顿力学,带负电的电子在围绕原子核转动时,应当发出彩虹那样频率连续的光辐射。而实际上观察到的,是一系列不连续的、完全独立的谱线,很像超级市场上用的“条形码”,只是带有颜色罢了。更糟糕的是,如果电子以经典电动力学预言的方式发出光辐射,则电子会失去能量从而螺旋式地掉到原子核上——就像水流进排水管洞口那样。从经典理论得出的不可避免的结果是,作为物质结构基本单元的原子,是不稳定的。
量子论的诞生
量子力学以一种迂回的方式,出来搭救这些自我毁灭的经典原子。它始于一个并非存心要闹革命的德国物理学家普朗克(Max Planck)。普朗克的工作实际上要比卢瑟福的原子模型早10年。当时所有的理论都不能够解释一个物体的温度和它发出的电磁辐射的量之间的关系:比如,一个烧红了的火钳,当再加热时为什么会变白。当时的理论学家是根据一种理想的模型来做出预言的,这种模型叫做“黑体”,它百分之百地发出或吸收辐射。在辐射谱的红端也就是低频部分,黑体模型与实验符合得很好。对于高频部分,它预言物体将发出无穷大的能量。这个荒谬的结果被戏称为“紫外灾难”。事实上,观测表明,辐射的密度在高频和低频端都很小,而在中间某个地方出现有一个峰,峰的位置决定于发出辐射的物体的温度。
到了19世纪90年代后期,人们把一些近似的定律拼凑在一起,用来拟合黑体辐射的实验测量结果。但是,对于辐射密度随着频率变化的规律,一直等到1900年10月19日,才由普朗克在德国物理学会的一次会议上,给出了一个令人满意的解释。他的这一个历史性的宣布,其根源要追溯到1897年他和玻耳兹曼的一次争论,在那次争论中,玻耳兹曼建议他用一种统计方法去解决问题。普朗克是当时最重要的热力学家之一,他自然希望热力学能够解决黑体问题。玻耳兹曼首先创立了一种统计力学方法作为热力学的基础,这种方法的根据是假设原子和分子存在。作为一个原子论的反对者,普朗克当时拒绝用这种方法。其实早在1891年的一次偶然见面中,玻耳兹曼就曾对普朗克和奥斯特瓦尔德谈到,在他看来,“没有理由认为,能量不是分成一个一个‘原子’的”。作为一个老派物理学家的普朗克,最终反悔而接受了玻耳兹曼的建议。他最后得到的定律对黑体谱给出了十分漂亮的描述。
为了导出他的定律,普朗克确实不得不假定,电磁辐射所携带的能量是一份一份的,他把这叫做量子。他发现,像物质一样,能量也只能被分成为有限的份数,而不是无限多份。他这个工作的中心点是一个数学关系,它表明,量子的能量可以用辐射的频率,乘以一个新的基本自然常数来计算,现在这个常数就被称为普朗克常数。能量和辐射频率之间的这一简单的“普朗克关系”,实际上说明了能量和频率是同一种东西,只不过是用不同的单位来表示罢了。
爱因斯坦出场
普朗克认为他对于黑体辐射的解释是古怪可笑的,因为它与经典电磁理论的教义相矛盾,所以他没有能够进一步地挖掘这一解释的更深的含义。作为一个保守的科学家,他只是把他的理论当做一种用起来方便的假设,而不是当做奥妙的真理。然而他也是一个务实的人,由于这个理论是这样卓有成效,他对它深信不疑。但是当他的理论的全部含义,后来被其他人详尽地加以阐明的时候,他还是受到了很大的震动。有人这样说,当普朗克把量子幽灵从瓶子里面放出来后,他被这个幽灵吓得要死。
再一次是爱因斯坦,他把这个理论向前推进了一大步。他对量子论做出卓越贡献是在1905年,在这同一年,他关于相对论和布朗运动的论文发表在《物理学年刊》上。实际上,正是由于他在量子论方面的这一突破而不是相对论,使他获得了1921年的诺贝尔物理学奖(这一消息是1922年发布的)。他这一成就解决的中心问题,是所谓的光电效应。实验表明,照射在固体金属表面上的光,可以使金属发射出电子。这些电子的能量不随光的强度变化,而是随光的颜色变化。这样的行为完全不能用经典的电磁理论来说明,因为按照这一理论,光的强度越大,从金属里面打出的电子的速度也就越大。但实际观测到的是,当颜色给定时增加光的强度,只会打出更多的电子,而电子的能量却保持不变。为了解释这个现象,爱因斯坦认为,能量是以微小份额的形式由光线携带的,他把这称为“光量子”。比较亮的光线表明有更多的量子——所以能从金属中打出更多的电子。频率比较高的光意味着更大的量子,所以逃逸出来的电子会具有更大的速度。在某一量子尺度下,电子就完全不能够获得足够的能量而离开金属表面。
对他这(完全基于演绎)的特殊解释,人们当时是表示怀疑的。因为尽管有普朗克早先的工作,但人们仍然普遍认为,电磁辐射的能量是连续的。爱因斯坦的建议在某种意义上是说,光是由微粒构成的,这是牛顿支持的一种观点,它早在1678年就已经被荷兰惠更斯的光的波动说所取代了。波动说看上去是如此优美,它清清楚楚地解释了一系列光学现象,例如折射、反射和干涉(当从两个光源发出的光迭加在一起时,就会发生干涉,这时候产生明暗相间的干涉条纹),因而使人们不愿放弃。
实验物理学家们用了许多年时间,详细地检验了爱因斯坦的光电效应理论。到了1916年,它被完全证实了。这个理论的非凡成功,最终迫使科学家们在20世纪20年代重新考虑光的本质。然而,令人啼笑皆非的是,这一理论与波动理论的冲突,却使爱因斯坦在其后半生中忧虑不安。他总是强调,光量子说只是一种暂时性的假定。1951年12月12日,那时他已近垂暮之年,他写给他的朋友贝索说:“这50年来,冥思苦想并没有让我接近这个问题的答案:什么是光量子?当今任何一个普通人,都认为他知道这个答案,但是他是错的。”尽管爱因斯坦本人的保留态度,光的这一独特的存在形式,今天已经被毫不含糊地证实了。光量子被命名为“光子”,这是物理化学家列维斯(Gilbert Lewis)1926年建议的。但是这并非意味着光不是一种波动。这是因为,光子在具有粒子性质的同时,也具有波的性质。它有时表现得像波,又有时表现得像粒子。这是我们第一次遇到的量子世界的奇怪特征之一:粒子和波的双重性。
波和粒子
波-粒子双重性对显示光的波动本质的经典实验来说,是一个意想不到的周折。这个实验是杨(Thomas Young)在19世纪初进行并分析的。他让从一个光源发出的光,投射到一个开有两条狭缝的不透明的屏上。这两条狭缝就像一个二次光源,光穿过它们之后继续传播,最后投射到一个屏幕上,形成明显的明暗相间的带状条纹,这是一种典型的干涉作用。这个实验是光的波动本质的一个很好说明:让一列并行的水波通过水中开有两条狭缝的屏障,也能够产生出类似的干涉图样。当水波从这对挨得很近的狭缝中通过后,有些地方的波相消,另一些地方的波相长,这就出现了动静相间的干涉条纹。
现在让我们想象,在杨做的实验中,如果我们只用一个光子,会产生什么样的结果。一个粒子的质量是集中在一个单独的点上的,而波是一种没有质量的实体,它弥散在一个有限的范围之内。这样,一个光子必然是只能穿过这两个狭缝之一。然而结果却是,如果我们把单独的光子一个接一个地向这两条狭缝发射过去,并记下它们到达屏幕的位置,最后我们会得到以前用一束光照射时那样的干涉图样。这样看起来,一个单独的光子,会由于它的波动性质而对两条狭缝都有感觉。
这种双重性质不仅仅是光才有——它含有更广泛的意义。这一点,是一个名叫德布罗意(Louis de Broglie)的法国年轻人顿然领悟到的。德布罗意出身于贵族家庭,他战时曾从事无线电方面的工作,这使得他的兴趣从中世纪教会历史转到物理学方面来。他主导法国物理学界的时间超过了一整代人(有人说这是件坏事)。他对于量子论的贡献是如此极端彻底,以致有人讽喻为“法国喜剧院”(法国资格最老的剧院,路易十四世创建于1680年——译者注)。德布罗意从光量子中认识到,正像光波可以表现为粒子一样,粒子也可以表现为波。为了使他这个直截了当的想法有一个坚实的基础,他提出了一个简单的数学关系,把一个运动物体的动量和与物体相应的波联系起来:这个“粒子”的波长反比于它的动量(即粒子质量和速度的乘积),这个比例常数再一次又是普朗克常数。这样,粒子的速度或者质量越大,它的德布罗意波长也就越短。
1923年德布罗意首次把他的想法写成三篇短文,发表在《巴黎科学院学报》上。然后他着手写他的博士论文,该论文于1924年完成。论文审稿人之一是朗之万(Paul Langevin),他显然对这一想法感到十分震惊。他把这篇论文的一份拷贝寄给了爱因斯坦,爱因斯坦马上认识到其中的意义,他在回信中说,德布罗意“已经把大面纱的一角揭开”。无疑地,爱因斯坦的这一评价对论文顺利通过口试起了影响。但是德布罗意并不希望仰仗爱因斯坦的权威——他向自己问道,如何才能够使这一想法得到验证。1927年,德布罗意的想法终于毫不含糊地被实验证实,其中一个是戴维森(Clinton Davisson)和盖尔末(Lester Germer)在美国贝尔电话实验室做的,另一个是由瑞德(Alexander Reid)在汤姆孙(George Thomson)的指导下,在苏格兰的阿伯丁大学完成的。非常有趣的是,以前J·J·汤姆孙曾因为证明电子是粒子而获得诺贝尔奖,而此时他的儿子却因为证明电子是波而获得同样的奖。
物质的粒子和波的双重性质具有奇异的结果。让我们想象一个“量子台球”游戏。球的波动性会产生许多令人惊异的后果。无论击球人瞄得多么准——例如,他瞄准一个在球袋边上的红色球——这个球却总有机会落到球台另一端的球袋(因为作为波,这个红球应该扩展到整个桌面)。由于一种叫做“隧道效应”的量子现象,也有可能直接越过另一个球,这时被击的球可以径直地穿过另一个位于中途的球。这同样是由于球的类波性质,使它可以扩展而跨越障碍物。
如果德布罗意的想法是对的,那么为什么我们在平常的台球游戏中,看不到这样的类波作用和其他的量子现象呢?这个原因可以从德布罗意关系中找到。德布罗意关系表明,粒子的波动性决定于它们的质量——质量越大则相应的波长越小。对原子而言,这一波长相对于它们的“尺度”来说很大,而对于通常的(宏观的)台球而言,这一波长就小到了微乎其微。只有把台球游戏缩小到微观尺度,我们才能够观察到这些奇特的量子效应。
玻尔原子和量子论
上面说的这些,和原子有什么关系呢?为了了解这一点,我们首先必须回到1913年,去看一下丹麦理论物理学家玻尔的研究工作。对于玻尔的才智有各种评价,它们之间有着天壤之别:卢瑟福把他形容为“我从来没有遇见过的最聪明的小伙子”;而伽莫夫却认为,玻尔的最大特点是“思维和理解的迟钝”。邱吉尔(Winston Churchill)也重复过同样的观点,他认为玻尔是一个枯燥乏味的人。然而,玻尔确实启发和主导了研究世界的新途径,这个新途径是由于量子理论而出现的。
针对经典力学不能对付卢瑟福的自我毁灭的原子,玻尔提出了一个尽管不优雅,但是带有根本性变革的解决办法,这个办法介于经典力学和现代量子力学之间。他对围绕原子核旋转的电子,简单地提出了一个人为的假定——用新的量子法则取代牛顿力学。这些法则不能真正称为运动定律,因为它们不具备任何理论基础。这些法则只是直截了当地说,电子占据着固定的轨道,在这些轨道上面它们不发出辐射。玻尔把这些轨道称作“稳定的量子态”。这个想法真可以说是无源之水、无本之术,它和爱因斯坦关于光电效应的想法有许多共同之处。
像以前认为的那样,电子在不同的轨道上运行,颇像围绕太阳的行星。但是当原子接收到电磁能量时,例如吸收了一个光子,则其中一个电子会立即跳到离原子核更远的另一个轨道上。这就解释了独特的分立谱线,因为只有当电子再跳回到它原来的轨道,即“稳定的量子态”时,才会有光辐射出来。这里我们可以看到量子体系的一个主要特征:能量不是以一种连续的方式被吸收或者辐射出来,而是只能在发生突然的量子跃迁时,按照原子的能级而改变。
玻尔把他的模型用于最简单的原子——氢。氢原子只有一个电子,围绕一个电荷量相等但电性相反的原子核作轨道运动。氢原子核的质量比电子要大得多,它称为质子,是卢瑟福在1919年发现的。玻尔运用他的量子法则,首次解释了氢原子辐射的电磁谱。现在物理学家们不仅可以搞明白,为什么氢原子的谱具有包含一系列分立频率的“条形码”结构(这些频率对应于电子的量子跃迁),而且对谱线出现的准确频率也可以做出预言(图9)。
虽然这个新理论是令人兴奋的,但它并没有能说明较为复杂的氦原子光谱。氦原子是仅次于氢的最简单的原子,它只有两个电子,围绕一个带两倍正电荷的原子核旋转。对于更复杂的原子,这一理论就显得更无能为力。除此之外,使玻尔理论从根本上失去效力的原因,是它没有解释这个人为的量子假定。这样,它只是一个不完全的,或者是一个临时性的原子结构理论。

图9 原子光谱的例子。吸收线或发射线出现在分立的光线频率处,这对原子的量子本质给出了强有力的证据。[录自W.J.Moore《物理化学》第587页]
新的力学
下一个突破过了一段时间才来临。这个突破,是几乎同时地由两条独立的途径得到的,其中之一是年轻的德国人海森伯(Werner Heisenberg),另一个是奥地利人薛定谔(Erwin Schrodinger)。
1925年,海森伯第一个得到了一个适合微观世界的量子表述形式,他称之为“矩阵力学”。他在北海的海尔古兰岛上染上了花粉热,康复以后,他就创造出这个世界上第一个完善的量子理论。他的理论之所以叫做矩阵力学,是因为它用一种叫做矩阵的数学形式来表述微观世界。矩阵的代数和通常的数字代数很相像,但是有一个很重要的例外。在通常的乘法中,二乘三和三乘二是一样的。但是矩阵A乘矩阵B,并不等于矩阵B乘矩阵A。后来人们认识到,这个不对称的数学特点联系着这样一个事实,即仅仅是测量的先后次序不同,微观世界就可能给出不同的结果。这是量子世界所显示的许多奇特性质之一。
矩阵力学相当抽象,所以薛定谔的表述方式更容易引人注目。薛定谔受到玻耳兹曼很深的影响,他自己说过,“玻耳兹曼的学说对我起的作用,就像科学上的初恋一样,没有其他任何学说能再使我如此入迷。”薛定谔1926年对原子问题的解释,被索末菲(Arnold Sommerfeld)称赞为“20世纪所有令人惊异的发现中,最令人惊异的发现”。
德布罗意的工作给了薛定谔极深刻的印象,所以他全力投入到这个波-粒子学说的研究中。他是在阿罗萨发展了波动力学的,那是个离滑雪胜地达沃斯不远的、阿尔卑斯山中的一个地方。当时他和他的情人在一起,因为那时他和他妻子的关系,处于他们婚后的最低潮。摩尔(Walter Moor)在他的薛定谔传记中写道:“像那个黑发女郎激起了莎士比亚诗创作的灵感一样,这个阿罗萨女人永远是个谜……不论是谁可能激发起了他的灵感,薛定谔的精力变得如此充沛,这的确是富有戏剧性的。他在1年的12个月中始终保持创造活力,这在科学史上是独一无二的。”薛定谔在1925年12月的一封信中,描述了他如何在为这新的原子理论而奋斗。他说,它一旦完成之后,会是一个“非常漂亮”的理论。
1921年薛定谔的创造性达到了顶点。为了使自己不受到干扰,他常常用珍珠把耳朵塞起来。那一年,他完成了六篇有关他的波动力学的主要论文,它们都发表在德国的《物理学年刊》上。
薛定谔的理论是用微分方程来表达的,比起海森伯的矩阵方法,它是一种更直观形象的描述。从数学上看,薛定谔和海森伯的表述截然不同,但是如薛定谔本人马上表明的那样,它们的结果是完全一样的:“这好像是,美洲是哥伦布航海越过大西洋而发现的,但同样勇敢的日本人,如果航海越过太平洋也会发现这块新大陆。”由于薛定谔的理论更直观、更灵活,因而人们更喜欢用它来研究量子力学问题。
德布罗意的工作表明,玻尔有关氢原子的量子法则,即必须有一系列固定的电子轨道,可以用围绕原子核的电子波来解释。这些波称为“驻波”,它类似于共鸣时,管风琴琴管中的那种波,或者小提琴琴弦被弓拉动时产生的波。在这些情况下,谐振的出现是由于管中或弦上恰好有整数个波。与此类似,只有某些德布罗意波长可以在原子周围产生出驻波。每一个波长的值对应于一个电子的“轨道”(图10)。
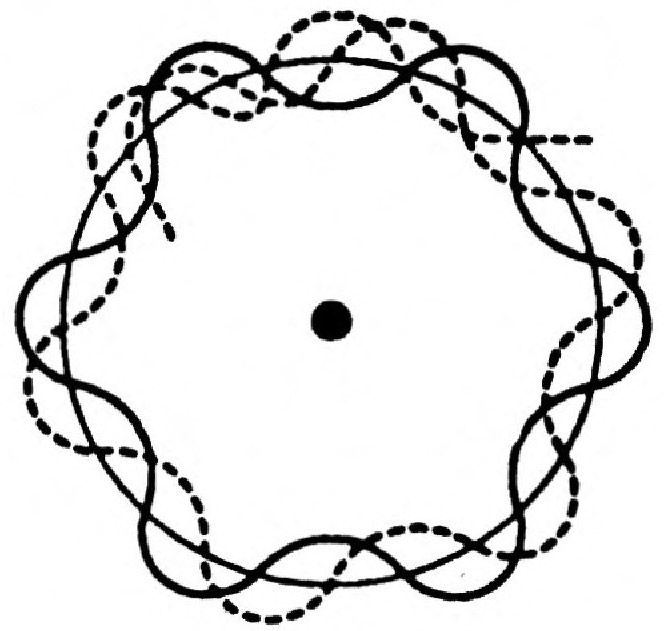
图10 德布罗意所想象的氢原子中的驻波(实践)。虚线表示非驻波将由于干涉而消失。[录自W.J.Moore《物理化学》第595页]
按照这种推理办法,薛定谔得到了一个方程,它描述物质波在微观尺度如何随时间演化。在本质上,这件工作与牛顿和爱因斯坦在他之前已经做过的一样。对牛顿和爱因斯坦来说,动力学的关键问题,是直接地描述像台球那样的物体,其位置如何随时间而变。然而,薛定谔的工作是对于微观尺度,这时候一个粒子也同时是波。这使得分析变得更错综复杂。因此,他的方程里面含有一个全新的数学量——“波函数”,它考虑了微观粒子的波粒双重性质,并描述它们所有可能的表现。为了使波动力学和日常现象相联系,薛定谔在构造波动力学时,使得它对于像台球这样的宏观物体,就化为类似于牛顿力学的方程。于是,“薛定谔方程”就成为理论物理和理论化学中,所有方程中最基本的方程。后来的一位量子论大师狄拉克(Paul A.M.Dirac),把薛定谔的这篇论文形容为:囊括了全部化学和大部分物理学。
为了验证他的方程,薛定谔把它用于氢原子中的电子波。从应用数学的角度来看,这个方程本身并不新奇。薛定谔用标准方法解出了这个方程,他发现,跟波尔的结果一样,他的结果也和光谱实验中氢原子辐射的能量严格相符。但是现在,支配着电子、使其仅仅占据固定轨道的量子法则,清清楚楚地摆在面前。与玻尔不同的还有,薛定谔现在可以分析并成功地解释有两个电子的氦原子。
虽然有这样的成功,薛定谔却搞不清楚波函数在物理上的含义。显然,他开始时是希望能回到旧的经典概念上去,因为经典概念来源于日常生活,图像十分清楚。但是波函数使他的这一梦想破灭了。大约6个月之后,在用薛定谔方程研究像原子或电子这样的微观粒子的碰撞问题时,德国物理学家玻恩作了一个非常大胆的假设。他提出,可以把波函数解释为某种“几率振幅”,用来计算在空间某一区域发现一个粒子的几率。他认为,波函数的平方就给出了在指定地点和时间,发现粒子的几率。
玻恩的这个解释,绝不是马上就被大家接受了。实际上,对他这个解释的争论延续至今。争论的焦点是,量子力学的含义究竟是什么。答案只会有两种可能的选择,一种是薛定谔方程是一个新的基本力学的基础,而且玻恩的解释意味着,我们只可以谈及原子和亚原子层次现象发生的几率,而不能准确地预言这些现象。这对于决定论和因果律具有深刻的意义。另一种是量子力学并不是真正基本的力学,而只不过是对我们还不完全了解的事情,做出统计说明的一种方法——这些事情在某种我们尚不清楚、更深的层次上,是严格决定性和因果性的,正如牛顿物理和爱因斯坦物理那样。
爱因斯坦正是在这一点上与新一代的量子力学分道扬镳。新一代量子力学采用上面第一种选择,而爱因斯坦却固执地坚持第二种:“上帝不会把世界当做骰子”,这是他在辩论时常说的一句名言。爱因斯坦认识到,波函数的几率解释虽然得到普遍赞同,但它从根本上破坏了因果律,而因果律是许多世纪以来联系原因和结果的观念。他在为纪念牛顿逝世二百周年而写的一篇文章中说:“牛顿理论的精髓可能会给我们提供力量,去恢复物理现实与牛顿教诲中最深奥的特点——严格的因果律——之间的和谐。”一件非常引人注目的事情是,德布罗意和薛定谔两个人,都对新物理学所走的方向持意味深长的保留态度。在一次与玻尔的著名交锋中,薛定谔说道:“如果我们仍然不得不去建立这种该诅咒的量子跃迁,那我当初真不该和量子论打交道。”但是玻尔、玻恩、海森伯和他们的弟子们,对此异议置之不顾。他们按照自己的方式,为这一学科的“正统”说法打下基础。今天他们的说法已被广泛接受,尽管实际上,它带来的问题和它给出的答案同样多。
无处不在,同时又无处在
量子论所描述的世界使人感到震惊,它的一幅图像可以用图11(b)所示的一个非常简单的实验来描绘。这是一个用电子来做的杨氏狭缝实验。电子源每次向两条狭缝只发射一个电子,狭缝后面是一只荧光屏S,它用一次闪光来显示电子到达了屏幕。在这个实验中,荧光屏上会出现一幅干涉图样,上面电子数目的分布与荧光屏上的位置有关。
我们回想一下,电子既不是粒子也不是波,但是具有两者的属性。如果电子是粒子,它只会或者打中障碍屏而被撞回,或者穿过两条狭缝之一,从而引起荧光屏X处或Y处的闪光[图11(a)]。重复做这个实验,将会在X处和Y处引起同样多的闪光。另一方面,如果电子是散布在空间中的波,则波状扰动将同时经过两条狭缝[图11(b)],正像池塘中水的涟漪相互重叠会发生干涉一样,电子波也会在屏幕上产生特有的干涉图样,呈现我们看到的强度的峰和谷。
量子力学到底预示了什么呢?像赌赛马,它仅仅给出了成败的几率,即使只有一个电子时也是如此。实际上,它给出的是电子到达屏幕上每一点的可能性。它能够绝对肯定地告诉我们的,仅仅是在什么地方不会发现电子。在这种情况下,如果把电子想象为点粒子,则量子力学就意味着,电子可以到达屏幕上任何一点,只是要除去按波解释时波的强度为零的那些地方,这些地方电子到达的几率是零。发现电子的几率随着屏幕上的位置的变化,与波的干涉所预示的波强度的变化完全一致。然而,电子最终是到达一个固定位置,而不是扩展到整个屏上。只有足够多的电子经过仪器时才能建立起干涉的图样。
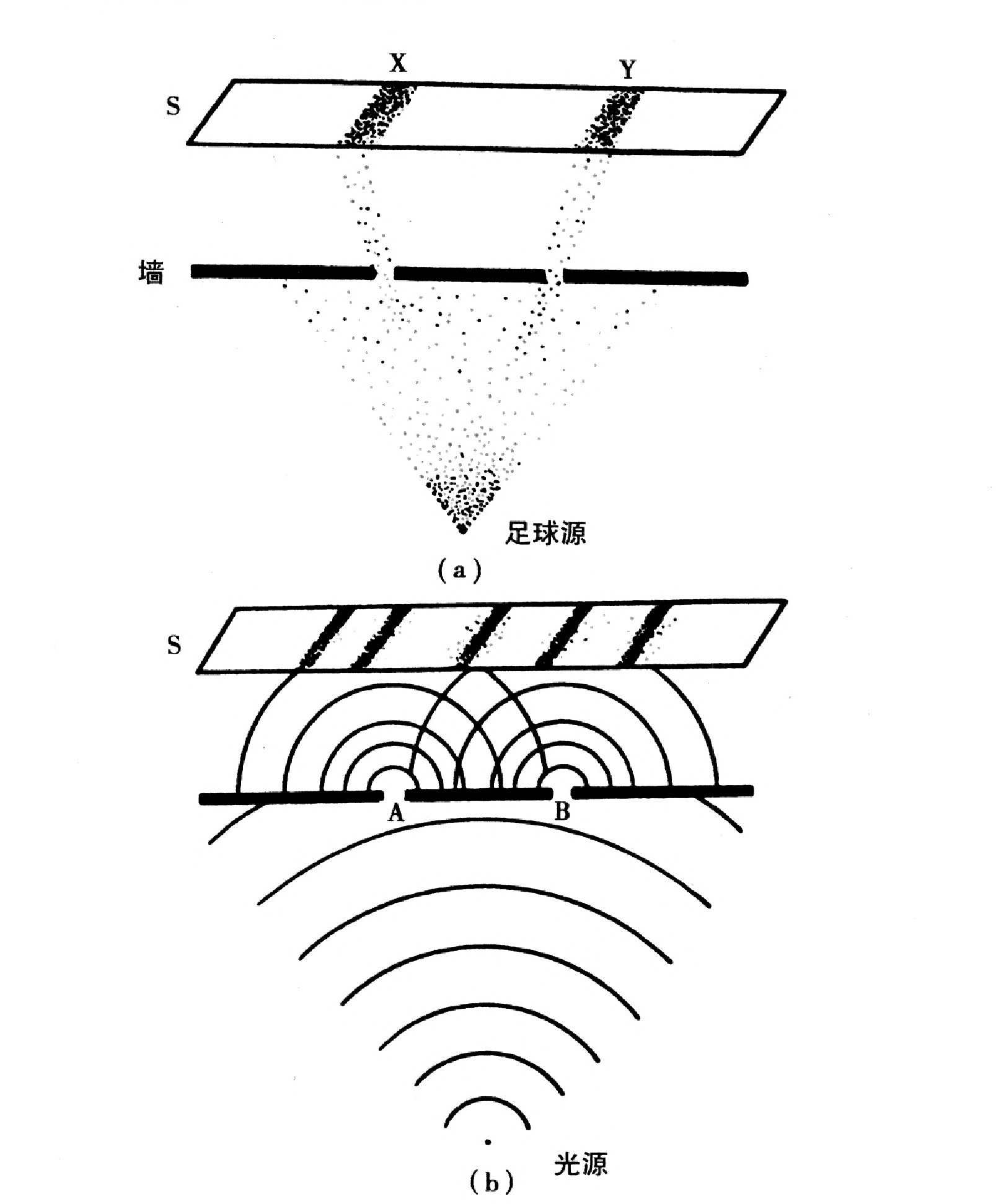
图11 (a)用经典粒子——足球——做的双缝实验,足球由源点踢出,穿过开有两条狭缝的墙而落到屏S上。球只能够达到X和Y处。(b)由一个波源发出的波,穿过开有两条狭缝的屏障,在屏幕S上造成的强度分布图样。屏幕上深色的区域相应于高的波强度,浅色的区域相应于低的波强度。缝A和缝B起着二次光源的作用。[录自J.D.巴罗《世界里面的世界》第134页。]
能够更清楚地显示这一点的量子力学的一个优美的表述形式,是美国理论物理学家费曼(Richard Feynman)在20世纪40年代提出的,当时他是普林斯顿大学的一名研究生。通常把这种方法称为“经历求和法”,它表明对物质世界的量子描述,当从微观领域进入到宏观领域时,是如何逐渐演变为牛顿的描述的。在费曼的描述中,一个量子粒子,比如一个电子或者一个光子,是尝试着通过源点和图11所示的屏幕到达位置之间,每一条可能的经典路径或轨道。因为粒子具有一个相应的德布罗意波长,每一个经典的“经历”都与其他的“经历”发生干涉,正如我们看到过的水波之间的干涉一样。这就导致了图11所示的微观粒子干涉图样的几率分布特征。但是如果使粒子的质量增加,比如增加到像足球那么大,则这种方法表明,相互抵消的干涉几乎在粒子所有的路径或“经历”上发生,只是严格地在牛顿力学所预言的路径(轨道)上面,不会发生这样的相消干涉。
如我们已经说过的,量子论不能够预言电子将到达哪里:它只是给出事件在给定地点发生的几率。这样,如果只有一个电子向狭缝发射过去的话,量子力学所能告诉我们的,是这个电子将会在荧光屏某个地方引起闪光,但波强度为零的那些地方除外。这种可能性如何变成现实性呢?闪光可能在屏上多处地方出现。然而,几率转变为确定性是由测量实现的:一旦在某个特定的地点发现电子,在其他地方发现它的几率就完全降到零。只有在实验重复大量次数的情况下,几率分布才变得有意义,也才能得到干涉的图样。
如果认为量子力学给出了最基本的描述,那么询问电子的行踪就没有意义,除非电子已经打到了屏幕上。因此我们只好得出结论说,电子是以某种方式扩散在空间和时间之中,它从两条狭缝中都穿过并且自己与自己发生干涉,直到最后奇迹般地瞬间瓦解在屏幕上某一点处,这地点完全是随机的。因而,我们可以说,电子是无处不在,同时又是无处在。
哥本哈根解释
玻尔大胆地正面处理了测量带来的难题。他的方法被大多数物理学家所采纳,被称为量子力学的“哥本哈根解释”,因为他一直在这个城市生活和工作。这一解释的基本前提是,我们对微观世界的描述受到我们语言贫乏的限制,而语言是建立在经由感觉传递过来的信息的基础上的。世界具有一个经典的部分,它由测量行为所构成;同时又有一个量子部分,这就是我们正在测量的东西。换句话说,我们所观察的世界看来是独立的实在,但它仍然是悬浮在某种“非实在的”微观世界之上。这种限制是避免不了的,因此我们不能希望去给出量子过程的一个真实的描述。玻尔的亲密合作者海森伯认为:“希望有新的实验能使我们返回到时间和空间上客观的事件,大概就像希望在没有探测过的南极区域找到世界的尽头一样,完全是梦想。”实际上,我们用以了解世界的观测必然是宏观的,我们也只能用这种宏观观测来讨论。按照玻尔本人提倡的极端说法就是,这种量子力学的解释认为,凡是不能测量的现象就没有客观的存在:“不存在量子世界。只存在抽象的量子描述。”
仅仅建议“基本粒子”、原子和分子没有独立的存在,就遭到了大多数物理学家、化学家和分子生物学家的诅咒。在这些确信原子实际存在的化学家和分子生物学家看来,这个建议无异于纯粹的左道邪说。然而,他们的模型所最终依据的量子理论,却不支持这样的原子实在的观念。伯克莱主教有一句名言,他否认牛津大学新学院的一棵树的存在,因为他是背对着这棵树。量子理论其实是伯克莱这种观点的现代版本。
按照哥本哈根解释,每一个观测必须由它的宏观环境所决定。测量过程本身在量子论中明显地具有相当大的重要性,而在经典物理中,它是被完全忽略的。
海森伯不确定性原理
在海森伯对量子力学的发展中,出现了另一个使人惊奇的特点。这就是他1927年提出的著名的“不确定性原理”。这一原理断言,自然界中存在一个测量精度的极限。设想一个像电子那样的物体从空间中飞过。按照经典物理学,它具有位置和动量,这两者可以被同时测量。而海森伯的原理简单说来,就是表明在亚原子领域,不可能同时精确地知道电子的位置和动量。如果想测量出某一时刻的准确位置,则它的动量(或者等效地,它的速度)就不能确定,反之亦然。
这个原理反映出波粒二象性佯谬:位置完全是一种粒子的典型性质,而波却没有准确的定位。波的特性知道得越多,可以谈论的粒子属性就越少。为了理解这一点,可以想象,当测量一个电子的位置时,会发生什么情况。例如,我们可以利用一个光子从电子处反射回来而做这个测量。虽然我们可以在某种确定的程度上,从光子最终的轨迹来推断电子的位置,但是在这个过程中,我们已经把数量不明的动量从光子转移到了电子身上。日常生活中也有类似的例子:测量一只轮胎的压力时,必然会使得一些空气逸出,从而使压力发生了改变。
总的说来,不确定性原理意味着,我们对一个量测量得越准,则另一个“共轭”量的不确定性就越大。把这两个不确定性联系起来的常数,又是我们的老朋友普朗克常数。因为它是如此之小,所以对于宏观物体,例如像台球或者牛顿的苹果,它实际上相当于零。因此,对于牛顿(以及相对论)力学所描述的物体,同时测量位置和速度并不受到限制。
海森伯的原理对时间的测量产生了一个后果。正如在任何情况下,我们不可能同时知道一个亚原子粒子的位置和动量一样,当我们在一段给定的时间间隔内测量能量时,这也有一个对测量精度的限制。按照不确定性原理,能量与时间之间的关系,和位置与动量之间的关系是一样的。对一个处在某一特定量子态的原子,能量的精确测量,必然要以原子处在这个量子态的时间——也就是它的寿命——的不确定性作为代价。反之,如果它的寿命已经知道得很准确,则它的能量就很不确定了。能量-时间的不确定性原理,对于宇宙学会有重要影响,我们稍后会看到这一点。有些人认为,这可能就是时间如何能够开始“滴答”的关键。
玻尔-爱因斯坦论战
爱因斯坦不同意不确定性原理是自然界的一个基本事实。如我们已经谈到过的,他宁可相信量子力学是一种数学手段,用以在统计意义上预言大量实验的结果,而不是对单一实验可能结果的最好描述。这导致了爱因斯坦和玻尔之间关于量子力学基本原则的一场著名论战,他们各自对于这一原则的看法,注定了他们此后的一生。有一次,在1930年在布鲁塞尔举行的第六次索尔维会议上,爱因斯坦提出了一个不用在实验室中进行的“思维实验”。他设计这个实验,是为了反驳能量和时间之间的测不准关系。但是,经过彻夜未眠的思考之后,玻尔设法借助于爱因斯坦最重要的发现之一——相对论,击败了爱因斯坦的挑战。但是故事远远没有结束。在玻尔1962年去世的第二天早晨,在他家的黑板上,人们发现画有一幅爱因斯坦1930年“思维实验”的图。看起来,玻尔直到生命的结束,还在同爱因斯坦的主张奋斗。
在开始的时候,爱因斯坦只是简单地认为新量子论是不正确的(自相矛盾的)。但是他在与玻尔的论战中屡屡败北,使他改变了他攻击的重点:他转而认为量子论不是不正确的,而是不完备的。他反对的理由,更多的是基于量子论明显地缺乏因果性,以及它与相对论原理的不相容。虽然他们之间的相互尊重并没有因为论战而动摇,但是爱因斯坦从来没有能够说服玻尔。这场较量折磨着他们两个人。有一位同事,也就是前面提到过的派斯,这样形容过玻尔有次在普林斯顿表现出来的苦恼:“他(玻尔)处在愤怒的绝望之中,不停地说‘我对我自己烦透了’……他们总是陷在关于量子力学意义的争论,并且一直到最后,玻尔也没有能够使爱因斯坦信服他的观点。”
这场大论战——爱因斯坦在其中扮演的是反对改革的角色——充满了讽刺性。我们已经看到,爱因斯坦在20世纪初期是如何因为他对自己的物理观念的自信而被孤立,尽管这种观念与当时成立已久的牛顿式传统观念完全冲突。由于他对光电效应的解释,他曾是量子理论的带头人。但是当新的力学在20世纪20年代中期破土而出时,他便不在带头人之列了。新理论的整个构思,完全和他的见解相对立。实际上一直到最后,由于他的自信,这个在把理论引导到现实方面做过诸多贡献的人物,却始终远离不断有所发现的现代物理的大进军。正像派斯所指出的,爱因斯坦对于量子论的观点“使他的形象从远远走在时代前面,一变而为处在时代潮流之外”。
然而,今天爱因斯坦也许有了雪耻的机会,因为有越来越多的科学家,对量子力学的基本原则提出了置疑。可能是由于时过境迁,离量子力学的奠基人和鼓吹者那个时代已过去超过一代人的时间,所以当今许多一流人才,并不是简单地接受传到他们手的那些卓越非凡的传统教条。在这些置疑中,一部分是围绕着探索对物理过程中时间作用的令人满意的解释。
时间:失而复得
初看上去,量子力学像它以前的理论一样,大大地削弱了时间箭头的基础。与像动量和能量这样的量比较,时间在量子力学中处于二级量的地位。利用称为“算子”的特殊数学工具,可以从波函数中提取可观测的信息。例如,从描写一个电子的波函数中,用这种算子可以得到位置或动量的值。但是并没有关于时间的算子,因为在量子力学中,时间并不被看做是一个“可观测量”(也就是可以测量的量)。由于这个原因,能量-时间不确定性关系的地位就有些含糊。但是,如我们将在第八章中看到的,如果时间之箭可以在一种广义量子力学中产生出来,则定义时间算子就变得可能了。
薛定谔的波动方程是决定性的,正像牛顿和爱因斯坦的运动方程一样。给定波函数在某个时刻的值,就可以严格地推断出任何或早或晚时刻的值。这个方程所描述的行为在时间上是完全可逆的。想象有一个特别的波函数,它在数学上代表一个没有观测到的电子的行为。这个波函数储存了有关这个电子命运的所有信息,一旦我们用某种测量手段去进行观测,例如用一个荧光屏,电子的行为就立刻显现出来。与此相同,这个方程使我们能够预言,如果我们在将来某个时刻进行观测,电子所有可能的行为。更重要的足,它使我们能够推断,假使我们在过去的某个时刻进行观测,电子当时所有可能的表现。只要我们仅仅是谈及几率和可能性——这一理论的看家本领——量子力学就是纯粹时间对称的。
在量子力学中同样也有一种斯多葛学派的永恒循环。量子理论运用于一个孤立系统时,会出现一种很强形式的(第二章中描述过的)庞加莱回归,这看来支持循环时间的观念。给定足够长的时间,一个孤立系统的波函数,例如宇宙的波函数,就可以回到它的初始状态。这样,量子力学并没有提供一个令人满意的基本原则,来解释时间的客观流逝,或者至少能把时间有意义地区分成过去、现在和将来。
当然,我们必须超越波函数——因为它只是包含一个系统的所有的潜在行为,而去发现在实验中实际发生了什么,也就是说,我们必须进行测量。从这一点上说,量子力学需要时间箭头。让我们回到外观上时间对称的波函数上来。当做出一个特定的测量时,会记录到电子已经到达某个地点,而且仅仅是到达这一个地点。这样,波函数——以及系统本身——必定在进行测量时经受了某种瞬时的转换。从一种反映所有可能结果的形式,变成只相应于实验中记录到的单一值,这是一个不连续的收缩。
这种从无数潜在的结果到观测结果的转换,称为波函数的“约化”或“坍缩”。如果我们采用量子力学的哥本哈根解释,可能发生的结果的数目会有无穷多个,但是当我们突然“碰”波函数时,其中只有一种结果变成为现实。想象你坐在一座量子剧院。这有无穷无尽、丰富多彩的剧目可能会上演,从莎士比亚到考沃德(Coward),到易卜生再到威尔德(Wilde)。但是一旦大幕拉开,剧院波函数坍缩,出现在舞台上的却是克里斯蒂(Agatha Christie)的“捕鼠夹”。
这样看来,如果我们背过脸去而且不偷看,波函数将以可逆的并且决定性的方式演化。然而对电子在屏幕上位置的一次测量,就会把波函数的行为改变成不可逆的。当波函数发生坍缩时,所有这许多的可能性就收缩为单一的现实结果。在系统过去状态(潜在性)和现在状态(现实性)之间的对称性,因而就被取消了。的确,如果试图从一个给定的测量结果去反推过去,就会得出不正确的结论。这样,测量操作本身,就把时间箭头引入到量子力学描述的现象中去了。
然而,无论是坍缩了的波函数,还是原来的波函数,都没有给出时间的方向。大多数物理学家,只是简单地采用数学家纽曼(John von Neumann,出生于匈牙利)所提出的一个补充假定,即波函数一观测就坍缩。坍缩的机制并没有给出来。确实,薛定谔方程本身显然并不能描述这样的坍缩,因为方程是可逆的而且是决定性的,而坍缩是不可逆而且是随机的。这就是测量问题的要害,它对于时间箭头具有极大的意义,并且引起了许多佯谬。
量子猫佯谬
这些佯谬中最著名的是薛定谔的“猫佯谬”。许多物理学家以恼怒的心情看待这个佯谬,因为他们认为这个佯谬并不具有任何“真实的”后果。例如,霍金有一次说过:“当我听说薛定谔的猫时,我就跑去拿枪。”所讨论的问题如果太深奥,这种不屑一顾的态度往往很普遍:很多人在一层薄冰上仍然轻松愉快地滑行,完全漠视脚下潜伏的危险。这样,猫佯谬就被认为是从量子餐桌上掉下来的碎屑,解决它是哲学家的事,而哲学家们也确实为此大动起脑筋。然而,也许有可能设计出实验来验证这个佯谬。
薛定谔所设想的“思维实验”如图12所示。一猫蜷伏在一箱子里面,而箱子中放有某种放射性物质,以及一个盛有致命的氰化物的小玻璃瓶。放射性衰变本身是一种量子过程,因此它的发生只能在几率的意义上加以预测。一种设计巧妙的连锁装置,使得当放射性样品中的某个原子发生衰变时,它触发的信号能使一把预先定好位置的榔头落下,打破小瓶使有毒气体逸出,从而把猫杀死。按照常识,猫是非死即活;但是按照量子力学原则,由箱子和其中一切物体所组成的系统,是由一个波函数来描述的。为使问题简化,让我们假设这猫只能存在于两个量子力学态——活或者死,系统的波函数中,就包含着这两种可能的、但相互排斥的观测结果的组合。因而这猫在同一个时刻是既活又死。如果我们这位老好人薛定谔教授不去打开箱盖看这猫,他自己的方程就表示,这猫的时间演化在数学上,可以用这两种状态的组合来描写,而这种组合在物理上(以及生理学上)是说不通的。正像在测量做出之前电子既不是波也不是粒子一样,这猫在教授最终决定去窥视它以前,既不是活着也不是死了。
薛定谔就是用他发明的这套“地狱般的装置”去抨击量子力学的非决定性,他把这非决定性从放射性衰变的微观尺度,转移到了死猫的宏观尺度。观测的作用不仅明显地在现象中注入了一种主观因素——某个人必须打开箱子去看这只猫,而且它也迫使猫不可逆地接受这两种可能性之一——要么玻璃瓶完好无损、猫也安然无恙,要么瓶子被打碎从而猫死去。

图12 薛定谔的猫和放置它的那个恶魔般的装置,箱壁假设是不透明的。如果箱壁是透明的,则按照量子基诺佯谬,放射性物质就永远不会衰变因而猫也永远不会死去。[录自《量子力学中的多世界论》(B.S.dewitt,N.Graham编辑)第156页。]
薛定谔的猫生动地把测量问题摆到我们的面前。看来我们得要相信,系统的状态被观测本身改变了。然而这显然又太离奇。如爱因斯坦所说:“我不可能想象,只是由于看了它一下,一只老鼠就会使宇宙发生剧烈的改变。”然而,即使是量子力学的先驱们,也没有把这当做必定是一件坏事。正像玻尔在与瑞士理论物理学家泡利(Wolfgang Pauli)的一次交谈中,对泡利说道,泡利的一个想法“是狂想,但狂得还不够”。
魏格纳的朋友
有两种简单通俗的办法,试图去对付爱因斯坦的异议。其中之一根据的是这样一种观念,即对量子系统进行测量的,不是猫或者老鼠,而是富于意识的人。这种想法的提出者中间,包括纽曼和魏格纳(Eugene Wigner),他们认为需要具有意识的观测者去“看”,从而影响波函数的坍缩;根据他们的看法,猫不具备观测者的资格以使波函数坍缩到生和死的真实情况,因为它并没有足够聪颖可以区分出这两种状态。按照这种观点,精神和物质是完全不同的观念,而且量子论只对后者有用。只有具有意识能力的精神才可以触动波函数。
这样就产生了一个推断,薛定谔的那可怜的猫,并不知道它自己是活着还是死了(纵然大多数宠爱猫的主人都声言,他们的宠物有和人类相近的智慧)。然而,动物是不是具有意识,这是一个极有争论的问题,起码这也是因为意识这个词本身就很难科学地下定义。它通常用来指人类那样的智慧,虽然这样一个泾渭分明的概念在这里很可能无助于事。
现在我们再来看“魏格纳的朋友”,他是这位诺贝尔奖获得者想象中的熟人。他的这位朋友戴着防毒面具,吃力不讨好地和猫一起关在箱子里。当他睁开眼睛时,猫的波函数就坍缩了。在薛定谔往里面窥视之前,这位朋友可以回答在箱子里面的感受。他可以用习惯的语言来报告发生了什么事——在箱盖未打开之前,他根本没有被卷入所有可能的实验结果的量子迭加状态。这样,按照魏格纳的说法,当人类的智能也包括到所研究的系统之中时,通常的那种量子描述就不能再用了。根据这种基于意识的量子理论解释,时间的流逝只不过是一种心理效果,它相应于不断地触动波函数。
人们可能会问道,魏格纳的朋友要喝多少升啤酒以后才失去知觉,从而失去触动波函数的能力。看来,我们现在很有回到一个极其主观的世界观的危险。正像雷(Alastair Rae)在他的《量子物理学:幻觉还是现实?》一书中所写道的:“自从现代科学四五百年前开创以来,科学思想似乎已经把人类和意识从世界中心远远移开了。宇宙中越来越多的事物,变得可以用力学和客观的术语来解释,即使人类本身,生物学家和行为科学家正在用科学的方法加以了解。而现在我们却发现,物理学——以前被认为是所有科学中最客观的科学,正在重新需要人的灵魂,并把它放置在我们对于宇宙理解的中心!”科学所积累的证据是如此之多,有利于一个独立于意识之外的现实存在,这使我们很难重视一个基于意识的处理量子理论的办法。确实,也许有一天,意识本身都会用物理学术语加以解释。
平行的宇宙
为了“解决”量子力学中的测量问题,埃弗雪特(Hugh Everett Ⅲ)1957年提出了另一个大胆的办法。他这个后来被科学幻想作家经常采用的想法,萌生于他在普林斯顿大学做博士研究期间,当时热心指导他的是惠勒教授。让我们回到杨氏狭缝实验并来考虑这两难推理,即光子到底是从两条狭缝中哪一条中经过。波函数中包含了光子从两条狭缝中经过的所有可能的结果,然而在最基本的层次上,对光子所经过的狭缝是要有一个选择。哥本哈根解释说,这就是按照几率法则对不可逆坍缩的选择。
然而,埃弗雪特的解释说,电子不是选择狭缝,而是选择宇宙。在选择其中一条狭缝而不是另一条时,宇宙就一分为二。这条被选择的狭缝决定于我们处在哪个宇宙。此后这两个宇宙就完全分开了,并且越分越多,每做一次测量,宇宙就分裂一次。埃弗雪特的想法关键是,宇宙自身是由一个波函数描述的,这个波函数中包含任何实验结果的组成部分。他的解释中有一个异乎寻常的含义——独立存在着无数“平行的”宇宙,每一个宇宙都像我们的宇宙那样真实。你做的最荒唐的梦,也许就发生在另一个世界。一个被定义在某个宇宙中的观测者,他所做的每次测量,都使这整个宇宙萌发出无数多个新宇宙(即“多重世界”),每一个新宇宙代表一个不同的、可能的观测结果(例如一活着的或死了的猫)。没有波函数的坍缩发生,只有新分支出的宇宙的无穷尽的增殖和萌发:不需要有一个宇宙之外的观测者。埃弗雪特的论文,与9世纪伊斯兰经院神学卡拉姆派的教义很有些相似:按照这个教义,随着每一个事件的出现,世界得以再生。
宇宙学家德威特(Bryce DeWitt)这样描述过他第一次听到埃弗雪特主张时所受到的震惊:“我仍然清晰地记得,当我第一次遇到多重世界概念时所受到的震动。100个略有缺陷的自我拷贝,都在不停地分裂成进一步的拷贝,而最后面目全非。这个想法是很难符合常识的。这是一种彻头彻尾的精神分裂症……”
许多宇宙学家偏爱埃弗雪特的多重世界量子力学解释,因为它不再明显地需要有一个外部观测者。这一点是重要的,因为如果采用魏格纳的解释,能够使传统的宇宙波函数坍缩的唯一观测者,必定是上帝。相比之下,埃弗雪特的主张看来是“在假设方面代价低廉,而在宇宙方面代价高昂”。有意思的是牛津大学的道奇(David Deutsch),他认为他所提出的量子计算机,一旦建造完毕,将可以从实验上验证埃弗雪特猜想的正确性。这种计算机具有许多新奇的性质,包括一种量子并行机制,使许多计算可以同时进行,而且计算速度也比通常的计算机快得多。道奇声称,这种奇迹般的快速计算,将需要把不同的计算部分放在一些平行的宇宙中进行。他的说法引起了很多争论,因为没有科学证据支持埃弗雪特的猜想,并且即使这样一种计算机造出来,也未必能证明多重世界一定就比其他解释优越。除此以外,多重世界的解释具有很多技术性的困难,特别是,它没有说明究竟是什么特殊原因,使得测量过程会导致宇宙的分裂。总而言之,它给人的印象是:杀鸡用牛刀。
读者存照
量子力学基于意识的解释和多重世界的解释,它们的牵强附会,反映着在现有的量子论的框架中,测量问题所引起的困难。基本问题被搞得含混不清,原因是人们广泛地、但错误地认为,传统的哥本哈根解释需要“观测者”的存在——这“观测者”被假定为人类,从而使主观因素乘虚而入。但是,其实并不需要有“意识”的生物参与:只要放上一套测量仪器,记录实验的结果就足够了。例如,这套仪器可以是由一台计算机,一个荧光屏,一张摄影感光乳胶片或是一个气泡室组成。人的意识与之无关。波函数的坍缩是不可逆的并且是完全客观的。
EPR佯谬
如果否定基于意识的解释和平行宇宙的解释,我们仍然面临着一个主要困难,即如何说明波函数的坍缩。这种坍缩看来违背了因果律常识——即果起于因,因果事件在空间上必须足够接近,以使得它们之间发生因果性联系。
考虑一个量子法则支配的系统,比如一个朝着荧光屏飞去的电子。它随时间的演化由一个量子力学波函数来描述,其演化规律遵从薛定谔方程。当在屏幕上做测量,以确定电子的位置时,波函数就坍缩了。虽然测量是在局部地点进行的,但是波函数的坍缩却改变了电子在此瞬间在空间所有地方的物理状态——要记得,波函数中包含了电子在空间和时间中的每一种可能性,并不只是波函数坍缩时的那一种可能性。
这种非局部的坍缩意味着违背了因果律。有一些时空区域,它们不能与屏上观测到电子的那个点有因果联系,即使信号以光速传播也不行。然而它们却可以在瞬间,和在这个地点所做的测量发生关联!电子发出的作用瞬时间达到宇宙的尽头,这听起来就像一位巫术师,能用针刺蜡像而伤害几千米以外的人一样,纯属天方夜谭。这一独特性质出现的原因,是由于波函数实际上是一种弥漫于整个空间的抽象场。一个在任何一个给定地点所做的观测,会引起一个潜在的状态(所有可能的结果)坍缩到一个现实的状态(观测到的结果),这个现实状态在宇宙中所有各处,并在同一时刻被固定下来。
这种离奇的非因果性的相关性,是1935年首次由爱因斯坦和俄国的波多尔斯基(Boris Podolsky),以及罗森(Nathan Rosen)在一篇论文中强调指出的,后面这两个人后来都成了普林斯顿高级研究所的成员。爱因斯坦本人是在1932年获得这个研究所的一个终生职位的,这使他逃脱了战前德国日益高涨的反犹太浪潮。这篇文章发表的时候他已经在普林斯顿定居,他的狭义相对论问世也差不多30年了。但是量子论仍然使他苦恼不安,一是量子论中的内禀随机性,二是现实看来是由观测者而“创生”的。对爱因斯坦来说,这种说法像是把人又推回到500年前宇宙中心的地位,而哥白尼当时就是把人从这个地位拉了下来。因而,爱因斯坦极力要把量子力学的这种观念推翻。
爱因斯坦和他的同事所构想的“思维实验”——取他们三个人名字的第一个字母,因而叫做EPR佯谬,是设想两个有旋转的粒子,它们相互作用并分离到无限远的距离。我们从它们相互作用的方式知道,每一个粒子具有一个等量但符号相反的“自旋”值:如果一个的自旋是“向上”,则另一个的就“向下”。这样,粒子A的自旋,就可以从粒子B的自旋推断出来。但是在量子力学中,两个粒子的自旋都处在一种不定的状态——“向上并且向下”——直到测量做出为止。测量使得粒子A的自旋在测量时刻成为“向上”或者“向下”,但是由于量子相关性,粒子B必须也立刻被迫接受一个确定的自旋,即与A的自旋相反。这一结果确保成立,不论粒子B与A的距离已经是多少个光年。我们不需要去测量B的自旋,因为一旦A的自旋测出,B的自旋也就知道了。这种遥远距离上鬼使神差般的作用看上去意味着两个粒子之间的联系,是由一种传播得比光还快的物理作用来进行的。
由这一分析可以看到,EPR佯谬的论点是,量子论不能给出一个现实存在的客观描述,并且量子论也是不完备的,因为它包含了如此非物理的、“非局部的”相关性。从那以后,很多研究都在探寻量子描述的某种更深一层的基础——即一种“隐变量理论”,它或许会以一种决定性方式说明这种相关性,并且可能进一步接受最后仲裁——即实验验证。这样的验证已经按照一个实际的EPR实验的路子搞了起来,它的结果会由于隐变量所支配或者是量子论所支配而有所不同。
对爱因斯坦和他的追随者来说不幸的是,量子论还是赢了。1982年,阿斯佩克特(Alain Aspect)和他的同事在巴黎理论和应用光学研究所证实,看来确实有一种超光速的联系存在于遥远的时空区域之间。两个在宇宙中远远分离的粒子,可以以某种方式组成一个单一的物理整体。这样看来,量子不确定性所暗示的那种疯癫独特的宇宙确是存在着:上帝的确是在把宇宙当做骰子玩耍。并且我们必须得出结论说,爱因斯坦所想象的、一个完全用科学描述的决定性实在,只是一个无法捉摸的幻想,它来自我们对世界的“常识”看法。
当时间停滞了
波函数坍缩的不可逆性,为时间之箭的客观存在提供了强有力的证据。然而,客观的波函数坍缩是以其特殊形式出现的,因而它不能对瞬息即逝的坍缩给出我们想要的完满解释。这一点可以从这个理论的一个显著特点看到,它表明,当一个量子系统被连续地观测的时候,时间实际上停滞了。让我们来考虑一个不稳定的原子核经历放射性衰变的情况,就像在猫佯谬中发生的那样。在量子论中,测量往往被理想化,是在某个固定的时刻进行的。但现在我们设想,原子核是在被连续地测量,目的是确定它究竟在哪个时刻发生衰变。
20世纪70年代,奥斯汀得克萨斯大学的米斯拉(Baidy-anath Misra)和苏达山(George Sudarshan)发现,在这样的条件下,原子核就不会发生衰变。这就像是把“盯着的水壶总是不开”这句谚语用到量子力学中来。连续的测量迫使原子呆在不衰变的状态,使它不能转换成衰变生成物。为了引起人们对他们的发现的注意,米斯拉和苏达山把这种现象称为“量子基诺佯谬”,因为它与基诺佯谬具有某些相似性。基诺佯谬是讲在空中飞的一支箭,但是根据他的分析,这支箭不可能在运动。然而,这量子力学中的比拟,并不能算是一个佯谬,它只是正统量子理论的一个推论罢了。
1989年在美国科罗拉多州波尔德的国家标准和技术研究所,有一个研究小组做了一次非常精妙的实验,实验结果支持了量子基诺效应。研究人员对放置在磁场中的5000个荷电铍原子进行了观测。这些原子开始时处于同一能级,由于一个射电频率的电磁场的照射,它们可以在0.256秒内“煮开”,即激发到高能级。只要在这当中不进行任何测量,所有的原子在照射之后都会位于高能级。然而,当用激光在这期间的某个瞬间进行探测时,研究人员发现,他们探测的次数越多,能达到高能级的原子数目就越少:当每隔千分之四秒进行一次探测时,就没有一个原子能够被激发。这样看来,一个被盯着的量子水壶是不会煮开的。
连续测量的概念,和分立测量一样,都是理想化的。任何实际的测量都只是持续一段有限的时间,这样,量子跃迁最终总会发生。这两种极端情况的结果显然都有些过于绝对:或者是某件事发生了,或者是什么事都没有发生。让我们再研究一下猫佯谬中那个凶神恶煞般的装置,但是把箱壁从不透明的换成透明的。这样我们就可以在所有时间中观察,到底箱子里面是怎么一回事。这时候量子基诺佯谬会说,只要我们保持观察(当然“我们”也可以换成为无生命的测量装置),猫就一定是活着的。看来,我们所谓的“伟大理论”确实是有问题。
薛定谔的猫、魏格纳的朋友以及其他佯谬,都突出地表明波函数的坍缩需要某种解释。在我们看来,出现这些困难的原因,是由于现有的量子理论是时间可逆的,而测量过程是内禀不可逆的。基于意识的解释和多重世界的解释,显然都是由来已久的削足适履之术。这表明,今天的量子理论还是不完备的。测量所造成的问题,只有借助于结合时间箭头的理论才能解决。我们将在第八章中讨论这一点。
物质和反物质
现在,我们还是继续对时间之箭的探索。一个对寻找时间之箭具有魅力的地方,是在亚原子粒子的奇异世界。我们所依据的基本原理,出自英国数学物理学家狄拉克(Paul Adrien Maurice Dirac),他在20世纪30年代量子论和狭义相对论相结合的过程中,起了关键性作用。开始的时候,狄拉克学的是电气工程师,但是他很快发现,他的爱好偏向于物理学。他有善做智力体操的令人敬畏的名声,以及怕羞、孤独的禀性。有一次,当他在多伦多大学作完演讲之后,听众中有一位加拿大教授问道:“狄拉克博士,我还没有搞懂,你是怎么样推出黑板左上角的那个公式的。”在一阵长时间沉默之后,并且也是在会议主持者的提醒之下,狄拉克这才回答说:“他说的不是一个疑问句,而是一个陈述句。”
薛定谔从一开始就认识到,他自己的方程有局限性——不满足爱因斯坦狭义相对论的要求(特别是,它不是洛伦兹不变的),而且它也不能说明原子光谱的精细结构。狄拉克针对这一问题,在1928年得出了一个相对论性的方程,它表明电子必须绕自己的轴自旋。除此之外,狄拉克方程的数学特点使他提出,应当存在正电子,这是“反物质”的一个基元。正电子的质量和电子的一样,但是电性相反。正负电子的碰撞会使得两者同时湮灭,而产生辐射爆发。安德森(Carl Anderson)1932年所做的一个实验,证实了正电子的存在,因而使反物质成为现实。这个发现从根本上改变了基本粒子物理的基础概念。在此之前,物理学家们对古希腊物质不变的观念深信不疑。这个实验之后,人们认识到物质可以任意产生和消灭。
根据狄拉克的数学描述,正电子被解释为如同它的反粒子——电子——在时间上向后退行。费曼甚至于提出整个宇宙中只有一个电子,它在时间上时而向前时而向后,轨道运动是如此复杂,使我们以为在任何瞬间都看到了大量单独的电子。像我们在第三章谈过的戈德尔的时间旅行一样,费曼的“一个电子”理论需要不同的时间方向同时存在,这导致与因果性观念的直接冲突,并且不可避免地,它产生的问题比它解决的要多。
在物质、反物质、空间对称性和时间的两个方向之间,存在着一个错综复杂的关系。它出现在一个奇特的CPT定理之中,这个定理是物理学微观定律数学形式的一个结果。CPT定理来源于一些定律的对称性,把任何过程中的粒子换成反粒子、把该过程换成它的镜像(即如同在一面镜子里看到的该过程)以及把时间倒转这三个变换同时操作的情况下,这些定律保持不变。这个定理是吕德斯(G.Lü iders)于1954年,泡利于1955年分别得出的。它的名字起因于三种抽象操作,它们的共同结果使得对称性得以保持:
◆C电荷共轭,它把物质转换成反物质;
◆P空间反演,它把空间坐标转换成它的镜像;
◆T时间反演,它把时间方向倒转。
CPT三重操作对于一个过程作用的结果,产生了另一个同样容许的过程,它也由同一理论框架所描述。不太严格地说,CPT定理断言,物理规律预言了在一种“泛镜像”世界中的等量但相反的事件。它同时可以告诉我们,时间对称性是如何可能被破坏从而产生出时间箭头。
CPT形式下的对称性可以用来演绎物理学。这样我们会发现,量子定律对于一个飞过球场的板球的描述,与对于这个板球的反物质的镜像在时间上倒退,最后飞回到投球手手里的描述是一样的。CPT定理最重要的一点是,如果所讨论的过程是CP对称的,则它必须也具有时间可逆的对称性(T)。这在本质上类似于,我们可以从一套餐具中餐叉的数目,推断出餐刀的数目。CP对称性还意味着,如果有一只反物质的左手戴着一块反物质的表,则一定会有一只正常物质的右手戴着一块正常物质的表;这样T对称性就表明,每一只表在时间上既可以向前走也可以向后走。相反的,如果CP对称性受到破坏——也就是反物质的左手不再有相应的正常物质的右手——则T对称性也要受到破坏:左手上戴的表在时间上就只能向前而不能向后。这看来就按归并派的想法,对于时间之箭在理论上给出了一个基本原理,它显然与前面谈到的测量问题完全无关。然而,几乎所有已知的“基本粒子”的相互作用都满足严格的CP对称性,因此它们对时间进行的方向并没有特别的要求,因为它们是时间对称的。
长寿K介子奇案
在微观“基本”粒了物理世界中,仅仅有一个奇特的现象,被认为是破坏了时间两个方向之间的对称性。这出现在一种不稳定的长寿K介子(K°)的某些衰变过程中。K介子是在美国的布鲁克哈文,由克里斯坦森(J.H.Christenson)、克罗宁(J.W.Cronin)、菲奇(V.L.Fitch)和特雷(R.Turlay)发现的。这一发现使克罗宁和菲奇获得了1980年的诺贝尔物理学奖。在大多数衰变中,K介子生成一个负的π介子、一个正电子和一个中微子,这一个过程的CP对称性被证明是保持不变的。然而K介子同样也可以衰变为(大约在10亿次衰变中有一次)一个正的π介子、一个电子和一个反中微子,这时候CP对称性就会受到破坏。按照CPT定理,T对称性在这罕见的过程中也就同样受到破坏:时间可逆的事件被禁止,过程成为不可逆的,时间箭头便显现出来。
在我们接受有时间意识的微观现象之前,哪怕这样的事例只有一个,我们首先应当探究CPT定理本身的正确性。CPT定理的证明是根据一些假定,但如果引力也包括在内的话,这些假定便不能满足了。然而,如果在这种罕见的过程中发生CPT对称性的整体性破坏(还没有观测到这种情况),这种破坏要比观测到的CP破坏还要小;因此T破坏一定发生了,虽然是间接地发生。彭罗斯评论说:“这几乎是完全隐藏着的时间不对称,它微小的作用看来在K介子衰变中是真实地存在着。很难相信,大自然不是在通过这一精美漂亮的实验结果,来试图给我们‘指点迷津’。”
但是,对这些内禀的时间不对称的相互作用,目前还没有令人满意的基本解释。因而还不能确定,是否长寿K介子的奇怪衰变将使我们对时间之箭的搜寻转向,或者如彭罗斯认为的那样,它将成为解释时间之箭的关键。这是因为,在本书以后要描述的一些熟悉的不可逆过程中,它并没有起到什么作用。
沸腾的真空
如我们已经看到的,海森伯测不准原理影响到时间的测量。在一个给定的时间间隔之内,我们所能够测量的能量的精度有一个限制。精确测定一个原子处在一个特定量子态时的能量,是要以处于这个态上的时间之相当大的不确定性作为代价。
下一节中我们会看到,一些宇宙学家相信,可以从这种不确定性中生出一个完整的宇宙。不确定性关系使得能量不能无中生有这个观念可以被违反。在经典物理学中,能量既不能创生也不能消灭,而是严格守恒的,只是从一种形式转换到另一种形式。例如,汽油中的化学能转变为热和汽车的运动。对于所有的初始能量,可以按这种方式做出一份能量平衡表。但是,如果时间间隔取得过小,能量守恒就会由于海森伯不确定性原理而受到破坏。
海森伯原理中的能量和时间的关系表明,所考虑的时间间隔越短,则能量的不确定性就越大。这使得能量守恒在非常短的时间间隔内不再成立:由于随机的量子涨落,能量可以从虚无中得到。这样的事件甚至可以在真空中发生,而按照经典的看法,真空是一无所有的。这样,量子论就给出了一个完全不同的真空概念。由于不确定性原理,真空实际上沸腾着活力。
现代的真空概念主要是狄拉克建立起来的。他认识到,如果要正确地描述物质吸收和发射光子的方式,麦克斯韦电磁场就必须用量子术语来描述。他推广了麦克斯韦的数学模式,把电磁场描述为数目巨大的振子的集合,每一个振子的能级都是量子化的,像原子中电子的能级那样。但是现在,由于不确定性原理,每一个振子的能量不能低于一个固定的最小值——即零点能,这就使得即使是真空也总是沸腾着活力:在空间所有各处,真空场的能量永无终止地在发生涨落。足够大的能量涨落可以使得粒子——反粒子对——例如电子——正电子对——在瞬息间生成,而且能量涨落越大,粒子对生成得就越迅速。这些真空量子场涨落具有相当重要的物理意义。例如,光子不断地产生和湮灭,可以触发吸收了能量的原子,使其自发地发出像光,即辐射。事实上,真空的涨落在某种程度上使虚无缥缈的以太重新受到注意,以太当时是被爱因斯坦当做一个多余的累赘,在1905年丢弃了。如牛津大学的史密斯(Christopher Llewellyn Smith)所说:“今天,我们对于真空一点都不懂。”
狄拉克把电磁场量子化以后解决了一些问题,然而却引起了更多的问题。简言之,困难的出现是由于场所能够携带的能量没有限制,这就导致理论中常常出现无穷大。正像广义相对论中奇点的情况一样,这种失控的行为在数学上是很讨厌的,并且它暗示着理论框架中什么地方有了问题。但是,在量子场论中,一些处理问题单刀直入的理论家,例如戴森(Freeman Dyson)、费曼、史温格(Julian Schwinger)和朝永振一郎(Sinitiro Tomonaga)发现了一种称为“重整化”的办法,可以用来克服这种发散困难。这种办法使得无穷大与另外的无穷大相抵消,因而被巧妙地吸收掉了。结果的形式给出了富于意义并且常常是非常成功的预言。但是,围绕重整化方法合理性的争论一直在继续;狄拉克本人就认为,无穷大问题是理论本身确实具有基本缺陷的征兆。甚至霍金都承认,重整化“在数学上是值得怀疑的”。
量子场论的主要缺点之一,是它不能处理引力。这时候产生的无穷大,即使借助于重整化技巧也无法消除。然而,宇宙学家们普遍认为,一个成功的量子引力理论,会解决我们在第三章中遇到的广义相对论的奇点问题。最近,出现了一种解决这个困难的新办法,即所谓弦理论。可以把弦理论看做是某种“高维”的场论,它的最小单元不再被看成是点,而是某种具有有限尺度的东西,即开放的或闭合的弦。这一理论的主要倡导者中间,有伦敦大学玛丽皇后学院的格林(Michael Green)和美国加州理工学院的施瓦兹(John Schwartz)。自从弦理论一问世,很多人都对它抱有乐观的希望,认为它将能够处理并统一包括引力在内的粒子间的基本相互作用,不会出现棘手的无法控制的无穷大。正因为如此,一些持高度乐观态度的物理学家,其中包括霍金,认为随着弦理论的出现,理论物理学的终点已经在望。
虽然从数学上讲,弦理论具有无可否认的美学上的吸引力,但在科学上还没有使人非相信不可的理由,能把它作为一种万能的灵丹妙药。用巴罗的话来说,“还没有实验上的事实证明它正确与否。在今后一些年里……一定会有这样的事实出现。只有在那以后我们才会知道,这一独特的处方是一种包罗万象的理论,还是一文不值。”尽管弦理论自己宣称可以解决许多问题,但是由于它的时间对称结构,它看来不大可能对时间的本质给出任何新的见解,特别是关于时间的方向,或者是与此有关的、然而常常被忽略的测量问题。
