伽利略在提出了相对性原理之后,觉得用一句话来表述这个原理还是显得不够简洁、不够酷。伽利略想,好歹我也是个数学家,怎么着也应该用数学的语言来描述我发现的这条伟大原理吧。于是没过多久,伽利略就提出了几个数学公式,用来描述相对性原理,后人把这几条数学公式就叫作伽利略变换式。在我们现代人看来,这个变换式其实是相当简单的,只需要用到一点点小学数学知识即可。现在我要给大家出一道小学数学的应用题(我相信这道数学题能勾起你很多美好的童年回忆):
小明和小红一起来到公交车站,两人见面以后互相对了手表确定时间。小红要坐的车先来,她登上公交车,车开动的时候刚好是7点整,公交车以10米/秒的速度开走了。问:1分钟以后小红距离小明多远?小红和小明的手表分别是几点?
可能你脑袋里会冒出一大堆问号,怀疑是不是我在出脑筋急转弯题。小明和小红的手表走时完全准吗?公交车走的是直线吗?小明在一分钟内确实没动吗?你这个距离是按照公交车头还是车尾算?小明是一直站着的吗?真的没趴下来?
我理解你这种心情,社会上混久了,总觉得简单的背后藏着什么陷阱。我现在很诚恳地告诉你,确实没有任何陷阱,忽略你的那些疑惑,这就是一道小学数学应用题。下面是解法:
1.一分钟等于60秒。小红距离小明的距离s=vt=10×60=600(米)。
2.小明和小红的手表都是07︰01。
上小学的时候,为了解这道题,老师一般喜欢给我们画一幅这样的图来解释:

【图2-3】数学题图示
看到这幅图,有没有勾起点童年的回忆?好了,从这道题出发,我们继续往下深入一步,我把这道小学数学题改写为一道初中数学题,如下:
小明和小红各自代表一个坐标系的坐标原点,且初始位置相同,有一只大懒猫在小明的坐标系中的坐标x处睡大觉,此时小红以速度v沿着X轴方向做匀速直线运动,t时间以后,设大懒猫在小红的坐标系中的坐标为x'(注意这个是x一撇),求x'和x之间的关系式以及小明的时间t和小红的时间t'之间的关系式。
我知道你对上面的题看了不止一遍,读上去有点拗口,看上去也有那么一点儿专业了,但这道题实质上和上面那道小学题是完全一样的,所要运用到的数学知识跟第一道题完全一样,我们看一下这道题的图解:

【图2-4】数学题图示
画完上面这个图解,我必须顺便提一下,像这样一根横着的X轴加一根竖着的Y轴的坐标系叫作直角坐标系,这是数学家笛卡尔发明的,我们在高中的时候还学到过一种极坐标系,那个只需要一个极点和一根极轴就够了(任何一个点的坐标是用到极点的距离和与极轴的夹角来表示)。直角坐标系因为特别容易理解,所以用得最广泛,以至于我们经常省略直角两个字,直接叫坐标系。我教你一个“装”的招数,就是下次遇到机会就这样说:“各位,首先让我们来构建一个笛卡尔坐标系……”加上笛卡尔三个字,听众立马就会觉得你很厉害。如果你只是平淡无奇地说:“各位,首先让我们画个坐标系。”这效果马上大打折扣。
言归正传,就着上面的图解,我直接写下答案,我想你一定能理解:
x'=x-vt
t'=t
以上这两个数学表达式我们称之为伽利略变换式。我知道你此时正在想:x'到x的变换马马虎虎还能算个数学公式,不过也真是够简单的,但这个t'=t真是要让我喷饭了,这算啥意思?就是告诉我们小明的手表过去了几分钟,小红的手表也过去了几分钟吗?这也需要伽利略当作一个伟大定理来告诉我们?
你先不用这么愤愤不平,让我来解释一下这两个数学表达式的伟大意义。坐标x我们可以把它抽象地认为是小明眼中的世界,而坐标x'可以抽象地认为是小红眼中的世界,有了这个关系式以后,只要知道了小红的速度和时间,我们就能把小红眼中的世界转换为小明眼中的世界。嗯,上面几句话我承认还是有点费解,所以需要来举例子。
现在你想象一下:小红在一艘匀速直线运动的船舱里做各种各样的力学实验,测量各种实验数据来推导各种力学定理。力学实验要测量什么?你仔细一想,会发现,所有的力学实验对于物理学家来说只需要测量两样东西,一个是坐标(比如小球的起点坐标和终点坐标),一个是用一个尽可能精确的钟表测量时间(当然通常还要测量一个质量,不过那个一般都是一次性测量或者取一个标准质量的物体)。所有的力学实验无非就是测量各种各样的坐标和时间的数据,然后从这些杂乱的数据中寻找普遍规律,从而总结出力学定律。
现在小红是一个在船舱中做实验的物理学家,小明是一个站在岸上的物理学家,对于同一个实验,小红以自己为参照系可以很方便地测量出来一堆数据,但是你想想如果小明也想测量小红所做的那些力学实验的数据,他该怎么办?小明既没有千里眼,也没有千里手,船每时每刻都在离他而去,小明对此只能望洋兴叹。
伽利略突然出现了,他看着愁眉苦脸的小明,微笑着说:“不用发愁,山人自有妙计。”
小明问:“什么妙计?”
伽利略:“你只需要知道船的速度即可,剩下的事情就都好办。”
小明:“船的速度不难知道,测出来以后接下来怎么办呢?”
伽利略:“你只要让小红把她测量到的所有实验数据下船以后给你,然后用我强大的伽利略变换式,你就能把她测得的所有坐标数据和时间数据变换成以你为参考系的数据。”
小明:“原来如此,伽利略你真了不起!”
于是,小明按照伽利略的办法如愿得到了所有他想要的实验数据。然后,小明和小红分别用自己手头的数据开始研究力学定律,研究完毕,两人把他们各自总结出来的规律一比较,竟然完全一致。
你看,有了伽利略变换式,我们就能证明对于同一个力学实验,不管是站在小明的角度观测,还是站在小红的角度观测,所得到的规律是相同的。这说的不就是伽利略相对性原理吗?看来伽利略还真是有点不简单。
大家应该还记得我们在上中学的时候学过一个关于自由落体的定律: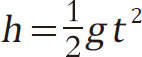 。这个定律告诉我们的是,只要知道物体下落的时间,就能算出物体下落的高度。
。这个定律告诉我们的是,只要知道物体下落的时间,就能算出物体下落的高度。
我本来想以这个为例子来说明虽然通过伽利略变换后实验数据的绝对值变了,但是最后用数学的方法倒腾来倒腾去,等式两边同时加加减减,居然所有的差异都神奇地抵消了,最后总结出来的公式,不论是在小明的参考系中还是在小红的参考系中都是完全等价的。但是考虑到很多人对数学公式的天生惧怕,我担心吓跑了各位耐心的读者,那就悲剧了!因此,我还是不卖弄数学风骚了。
伽利略变换式的伟大意义就在于,他用数学的方法证明了伽利略相对性原理。
说到这里,我相信各位读者已经完全理解了伽利略相对性原理和伽利略变换,一点儿都不难。正因为简单好懂,符合我们日常生活中观察到的所有现象给我们造成的印象,因此,伽利略大侠的这一原理,一变换就像是倚天剑、屠龙刀,统治了物理学江湖长达二百多年之久。在二百余年的时间里,无人不臣服,无人敢挑战,就好像此刻的你不也认为这是天经地义的吗?难道这真有可以挑战的地方吗?是的,二百多年后一个叫洛伦兹(Lorentz,1853-1928)的侠士拿着一把锈迹斑斑的大刀,向伽利略变换发出了挑战,并且竟然一刀就将伽利略变换这把屠龙刀斩为两截。随后,又有一个26岁的年轻人,无门无派,不知道从何方冒出来,携一把木剑向伽利略相对性原理这把倚天剑发出了挑战,这一战可谓刀光剑影,霹雳惊雷。这个年轻人,姓爱因斯坦,名阿尔伯特,那真是五百年一遇的一位奇男子。当然,这些是后话,且听我慢慢道来。
1642年1月8日凌晨4点,在故乡意大利,78岁的伽利略走到了人生的尽头,他不断地重复着一句话:“追求科学需要特殊的勇气。”声音越来越轻,终于,伽利略吐出了最后一口气,合上眼睛,一位科学巨星陨落了。冬去春来,斗转星移,整整一年后,在英格兰的林肯郡有一名男婴呱呱坠地,一位新的科学巨星诞生了,力学的接力棒从伽利略手上交到了这名男婴的手上,这名男婴叫作艾萨克·牛顿。
