这个世界已经变得越来越神奇了,连光线都不再是直的,但这又不由得我们不信。还有更神奇的,爱因斯坦用一个非凡的思维实验论证了这样一个事实:引力其实造成的是时空弯曲,也就是时间和空间同时被弯曲了。这下你的脑袋彻底晕了,你完全无法想象出时间和空间弯曲是什么概念,如果我说时间变慢,甚至说时间膨胀、空间收缩什么的,你大概觉得还马马虎虎能想象得出来,但是这个时空弯曲实在太令人费解了。别慌,爱因斯坦这个非凡的思维实验叫作“爱因斯坦圆盘实验”。“有趣啊,”你心里想,“前有牛顿水桶实验,后有爱因斯坦圆盘实验。干脆我们把有趣进行到底,把Tom和Jerry再次请出来吧。”你的主意很好,我这就请出这两位小家伙,这回让他们担任爱因斯坦的学生,一起来做这个思维实验。
爱因斯坦:“欢迎Tom和Jerry来到我的广义相对论大讲堂,本次讲课包你们满意。”
Tom托着腮帮子:“我讨厌上课。”
Jerry眯着眼睛:“能再睡会儿吗?”
爱因斯坦:“你们听我说,这堂课我们不在教室里上,我们去太空中上,怎么样?”
Tom和Jerry:“太空?哇,太好了!怎么去?快走快走。”
爱因斯坦:“请你们闭上眼睛,准备好了吗?般若波罗蜜!”
Tom和Jerry突然感到自己漂浮起来了,睁开眼睛一看,三人已经悬浮在漆黑的太空中了,四面八方全是星光点点。
爱因斯坦:“现在,我需要把你们俩放到一个特殊的、非常好玩的转盘游乐机里面去。”
Tom和Jerry:“在哪里?在哪里?”
爱因斯坦:“巴巴变!”
突然,三人眼前突然出现了一个巨大的转盘,就好像一个超级巨大的圆形饼干铁盒。
爱因斯坦:“这就是我们要去上课的地方,你们俩进去。因为我是这里的上帝,所以,你们俩的一切行动我都能看见,你们能听到我说的话,我也能听见你们说话。好了,现在给你们发道具,一人一只原子钟和纳米尺,这可是全世界最精确的时钟和量尺,千万要保护好。”
Tom和Jerry接过钟和尺,丈二和尚摸不着头脑,完全不知道爱因斯坦教授有何用意。先进去再说,看看有什么好玩的。于是两人抓着“饼干盒”的门框,稍一用力,轻轻巧巧地就漂进去了。
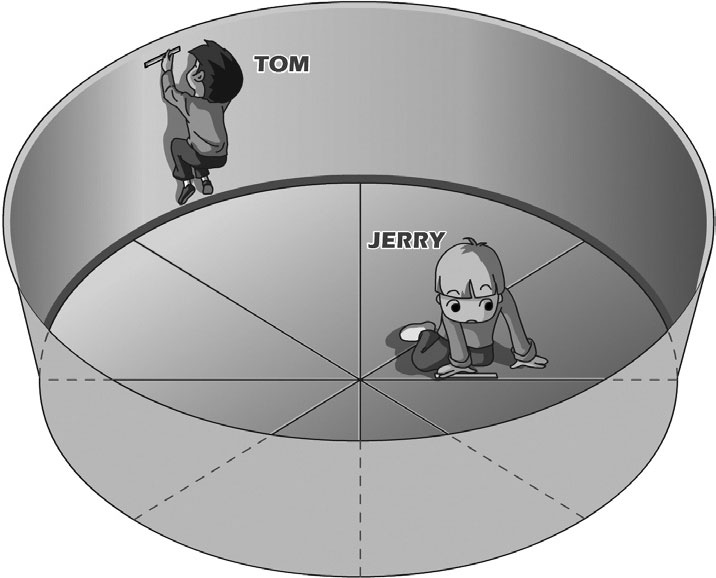
【图5-4】爱因斯坦圆盘实验
爱因斯坦:“Tom,现在请你在圆盘的内壁上就位;Jerry,请在圆盘底的圆心就位,我们的实验马上就要开始了。”
Tom:“这让我想起了我家关小白鼠的笼子里那个轮盘。”
Jerry:“这让我想起了我小时候最喜欢玩的东西。”
爱因斯坦:“请注意,我马上就要把它旋转起来了,你们准备好了吗?”
Tom和Jerry:“准备好了。”
爱因斯坦手一挥,整个转盘飞快地转动起来。
Tom由于是在圆盘的内壁位置,瞬间就感受到向心力。从我们观众的角度来看,他感受到的是向心力,但是对Tom自己来说,他根本分不出是重力还是向心力。且看我们的Tom怎么说。
Tom:“啊哈,我们是不是回到地球上了?我突然就感觉回到了地面,能正常走路了。”
爱因斯坦转身面向观众,解释说:“匀速圆周运动的实质是一种加速运动,根据我的等效原理,加速度和重力是一回事,所以Tom感受到了像在地球上一般的重力感。”
Jerry站在圆心的位置,所以他相对观众来说是静止的,Tom在Jerry周围一圈圈地转着。且看我们的Jerry是怎么说的。
Jerry说:“我没有感觉到任何变化,这里能见度不够,我甚至连Tom都看不到。”
爱因斯坦再次转向观众,解释说:“Jerry就好像处在引力的边缘一样,他此时仍然是悬浮在太空中的,没有受到任何引力的影响。我们用这样一个旋转的圆盘创造了一个小小的人工引力场环境。接下去,我们就要研究这个引力场对我们的时间和空间到底造成了什么样的影响。先让我们来研究一下相对比较容易研究的时间问题。”
爱因斯坦转过身去对两人问道:“Tom和Jerry,请你们告诉我,你们的原子钟的时间是多少?”
Tom:“11点55分,教授。”
Jerry:“12点整,教授。”
爱因斯坦解释说:“很好。大家请注意,Tom相对我们在运动,而Jerry相对我们则是静止的,根据狭义相对论的时间膨胀效应,运动会使得时间变慢,因此,我们可以很容易得出结论,那就是Tom的时间变慢了。但现在请大家把视角放回到Tom身上,对Tom来讲,他感觉自己并未运动,只不过是受到了引力而已,因此Tom可以得出这样的结论——引力使得时间膨胀了。让我们继续往下深入研究。”
爱因斯坦对Jerry说:“Jerry,现在我要你沿着圆盘上的径线往前去一点点。”
Jerry往前挪了一点点,突然就感受到了一点轻微的引力,这股引力在把他向远处拖拽,Jerry赶紧打开了绑在腰上的推进装置,以维持平衡。
爱因斯坦:“Jerry,请你再告诉我你的时间。”
Jerry报了一个精确的数字,爱因斯坦发现比自己的原子钟慢了1秒钟。
爱因斯坦:“很好。Jerry,请你继续沿着径线朝前挪一点,跟刚才挪动的距离一样,再告诉我时间。”
Jerry照做,又报了一个精确的数字。
这次比爱因斯坦的原子钟时间慢了2.5秒。
爱因斯坦继续指挥着Jerry一点点朝前挪动,每挪一段距离,就报一个时间,爱因斯坦记下每次Jerry时间变慢的幅度。
爱因斯坦解释说:“Jerry的时间为什么会变慢,道理很简单,Jerry一旦离开了圆心,他就会产生速度,所以时间就会变慢,而且他的线速度是随着离开圆心的距离不断增大的,因此他的时间变慢幅度就会逐步增大。现在让我们构建一个笛卡尔坐标系,把X轴当作距离的变化,Y轴当作时间变慢的幅度大小,然后我们把刚才Jerry告诉我的所有数据用一个个点标在这个坐标系里,最后把这些点用线连起来,我们很快就会发现,这是一根抛物线,一根完美的曲线。换句话说,随着离开圆心的距离增大,引力会逐步增大,而时间会逐步变慢,但时间变慢的幅度是一根曲线。我们可以这样理解,在圆盘上时间弯曲了;进一步说,也就是引力使得时间弯曲了。”
你禁不住鼓起掌来,太精彩了,爱因斯坦不愧是大师级人物啊,我似乎明白了时间弯曲是怎么回事了。继续继续,那空间弯曲又该怎么理解呢?
爱因斯坦:“Tom和Jerry,请拿出你们的纳米尺,不要告诉我你们弄丢了,那一把尺子可要花去教授我一个月的薪水呢。”
Tom:“教授,尺子在手里呢,让我做什么?”
Jerry:“这把尺子真好看。”
爱因斯坦:“Jerry,我要你现在开始量一下圆盘的半径长度。Tom你呢,就帮我量一下圆盘周长,就是你刚好走一圈的长度。”
不一会儿,两人都把数字报过来了。爱因斯坦用Tom量的周长除以Jerry量的半径,得出的数字发现比2π要大,这是怎么回事?
爱因斯坦解释说:“请注意,从我们观众的角度看起来,Tom由于在运动,那么根据狭义相对论,在运动方向上就会发生尺缩现象,所以Tom手里的那根纳米尺就会缩短一点点。而同时,Jerry是在沿着径线方向丈量,在这个方向上,纳米尺没有运动,自然也就不会发生尺缩现象。于是,Tom量出来的周长就会比静止时长一点点,而Jerry量出来的半径则不会变化。于是,奇怪的事情发生了,这个转动的圆盘的圆周率大于π。我们进一步想下去,在这个圆盘的人造引力场中,所有以Jerry为圆心的半径不同的圆都可以用同样的方法得出圆周率大于π 的这个惊人事实。观众们,你能告诉我在什么情况下一个圆的圆周率大于π吗?”
一个聪明的观众说道:“我知道,我知道。”
爱因斯坦:“请讲。”
观众:“圆规的质量不过关,不小心把圆画成了椭圆的情况下。”
爱因斯坦:“拜托,我们这不是脑筋急转弯呢,不考虑这种意外误差情况。”
观众一脸不好意思:“那我就不知道了。”
爱因斯坦:“如果你在一张纸上画一个标准的圆,圆周率自然是π。但是,如果你在一个篮球上画一个标准的圆,然后去测算一下的话,就会发现篮球上那个圆的圆周率小于π。同理,如果你在一个马鞍面上画一个标准的圆,则圆周率就会大于π。观众们,我们的结论就是,如果在一个曲面上画圆,圆周率就不会等于π。由此可见,在圆盘引力场中,我们发现圆周率大于π,这说明这个圆盘引力场中的空间并非平直,而是——弯曲的。”
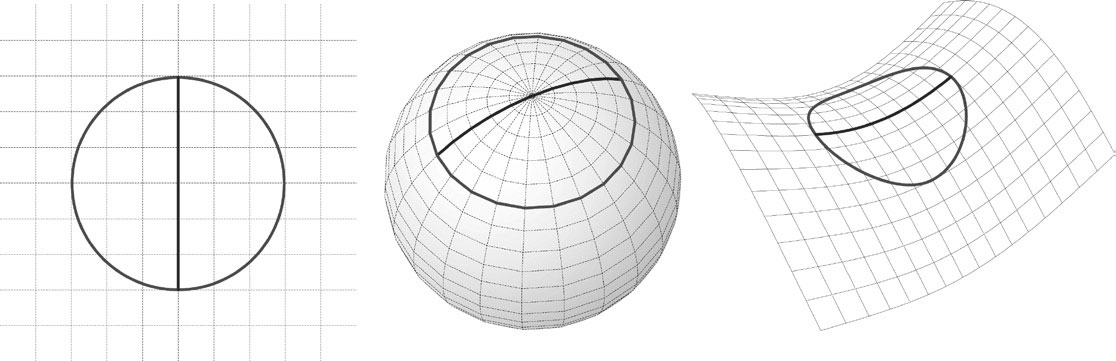
【图5-5】平面上的圆、球面上的圆、马鞍面上的圆
你再一次禁不住鼓起掌来,真是精彩啊!其实我在理解了爱因斯坦的这个圆盘实验后,也是禁不住大声喝彩,这实在是一场思维的盛宴。你马上就想到:我这么抬起手来,朝空中一劈,使一招“扭转乾坤”,显然我的手劈下去不是匀速直线运动而是加速运动,那岂不是我这一招真的可以把时空给弄弯曲了?没错,你的思考完全正确,只是你这一劈造成的时空弯曲效应,恐怕要把你的手放大到银河系那么大才有可能被察觉到。
作者注:本文所举的例子来源是美国物理学家格林的科普著作《宇宙的琴弦》(湖南科学技术出版社),对于这个例子,格林有一段注释,现基本原文引用如下:
关于所谓“刚性转盘”(即太空大圆盘更科学的叫法)的分析,很容易引起混乱。实际上,在这个例子中,许多方面到今天也没有达成一致意见。正文遵从了爱因斯坦本人的分析精神,现在我们还是照那个精神来澄清几点可能会令人迷惑的性质。第一点,也许有人奇怪,为什么转盘的周长不跟尺子一样产生洛伦兹收缩,那样Tom测量的周长应该和我们原先看到的一样。不过应该记住,那个转盘在我们的整个测量过程中都是旋转着的;我们从来没有分析过它静止的情形。这样,从我们静止观察者的立场看,我们的测量与Tom的测量的唯一区别是,他的尺子发生了洛伦兹收缩。我们测量时,转盘在旋转,我们看到Tom测量时,转盘仍然在旋转。由于我们看他的尺子收缩了,所以认为他需要多测几步才能测完一个周长,那当然就比我们测量的长。只有当我们比较转盘在旋转和静止的性质时,转盘周长的洛伦兹收缩才有相对意义,但我们并不需要这种比较。
第二点,虽然我们不需要分析静止的转盘,你可能还是想知道,假如它慢慢停下来,会发生什么事情呢?看来,这时候我们应该考虑由于不同旋转的洛伦兹收缩引起的随速度的改变而改变的周长。但这如何与不变的半径一致呢?这个问题很微妙;回答这个问题的关键一点是,世界上并没有完全的刚体。物体可以伸长或者收缩,从而能够协调我们看到的伸长和收缩。假如不是这样,就会像爱因斯坦说的那样,通过熔铁在旋转运动中冷却形成的转盘将因后来旋转速度的改变而断裂。关于刚性转盘历史的详情,请看Stachel,“Einstein and the Rigidly Rotation Disk”(爱因斯坦与刚性转盘)
